Egy iskolai tanulmányi verseny döntőjébe 30 diák jutott be, két feladatot kellett megoldaniuk. A verseny után a szervezők az alábbi oszlopdiagramokon ábrázolták az egyes feladatokban szerzett pontszámok eloszlását:

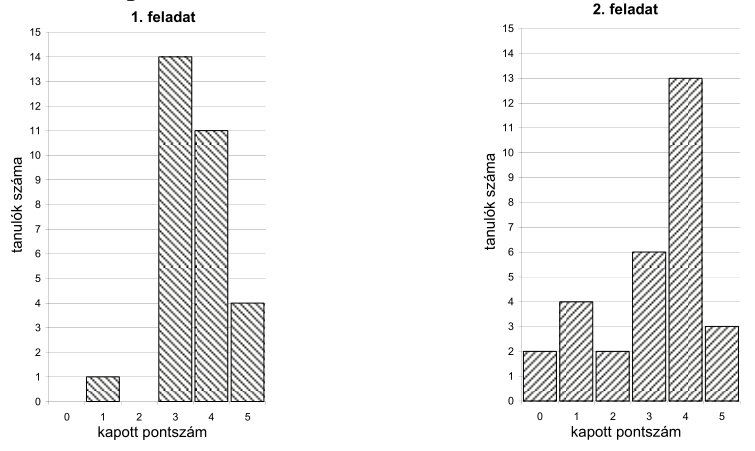
a) A diagramok alapján töltse ki a táblázat üres mezőit! Az első feladatra kapott pontszámok átlagát két tizedes jegyre kerekítve adja meg!

b) A megfelelő középponti szögek megadása után ábrázolja kördiagramon a 2. feladatra kapott pontszámok eloszlását!

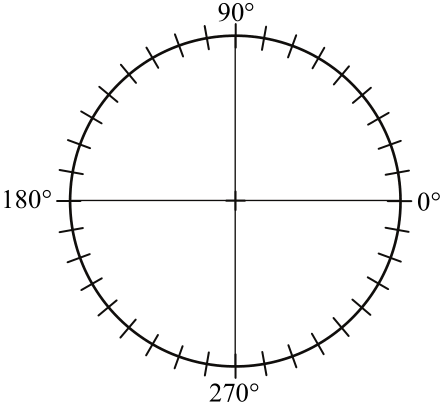
c) A versenyen minden tanuló elért legalább 3 pontot. Legfeljebb hány olyan tanuló lehetett a versenyzők között, aki a két feladat megoldása során összesen pontosan 3 pontot szerzett?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy autó ára újonnan 2 millió 152 ezer forint, a megvásárlása után öt évvel ennek az autónak az értéke 900 ezer forint.

a) A megvásárolt autó tulajdonosának a vezetési biztonságát a vásárláskor 90 ponttal jellemezhetjük. Ez a vezetési biztonság évente az előző évinek 6 %-ával nő. Hány pontos lesz 5 év elteltével az autótulajdonos vezetési biztonsága? Válaszát egész pontra kerekítve adja meg!

b) Az első öt év során ennek az autónak az értéke minden évben az előző évi értékének ugyanannyi százalékával csökken. Hány százalék ez az éves csökkenés? Válaszát egész százalékra kerekítve adja meg!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az ABC háromszög csúcsainak koordinátái: A(-3; 2); B(3; 2); és C(0;0).

a) Számítsa ki az ABC háromszög szögeit!

b) Írja fel az ABC háromszög körülírt körének egyenletét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy 12 cm oldalhosszúságú négyzetet megforgatunk az egyik oldalával párhuzamos szimmetriatengelye körül.

a) Mekkora az így keletkező forgástest térfogata és felszíne? A felszínt egész $ cm^2 $-re, a térfogatot egész $ cm^3 $-re kerekítve adja meg!

Ugyanezt a négyzetet forgassuk meg az egyik átlóját tartalmazó forgástengely körül!

b) Mekkora az így keletkező forgástest térfogata és felszíne? A felszínt egész $ cm^2 $-re, a térfogatot egész $ cm^3 $-re kerekítve adja meg!

c) A forgástestek közül az utóbbinak a felszíne hány százaléka az első forgatással kapott forgástest felszínének?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy új típusú, az alacsonyabb nyomások mérésére kifejlesztett műszer tesztelése során azt tapasztalták, hogy a műszer által mért $ p_m $ és a valódi $ p_v $ nyomás között a $ \lg p_m=0,8 \cdot \lg p_v+0,301 $ összefüggés áll fenn. A műszer által mért és a valódi nyomás egyaránt pascal (Pa) egységekben szerepel a képletben.

a) Mennyit mér az új műszer 20 Pa valódi nyomás esetén?

b) Mennyi valójában a nyomás, ha a műszer 50 Pa értéket mutat?

c) Mekkora nyomás esetén mutatja a műszer a valódi nyomást?

A pascalban kiszámított értékeket egész számra kerekítve adja meg!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

András, Balázs, Cili, Dóra és Enikő elhatározták, hogy sorsolással döntenek arról, hogy közülük ki kinek készít ajándékot. Úgy tervezték, hogy a neveket ráírják egy-egy papírcetlire, majd a lefelé fordított öt cédulát összekeverik, végül egy sorban egymás mellé leteszik azokat az asztalra. Ezután, keresztnevük szerinti névsorban haladva egymás után vesznek el egy-egy cédulát úgy, hogy a soron következő mindig a bal szélső cédulát veszi el.

a) Mennyi a valószínűsége, hogy az elsőnek húzó Andrásnak a saját neve jut?

b) Írja be az alábbi táblázatba az összes olyan sorsolás eredményét, amelyben csak Enikőnek jut a saját neve! A táblázat egyes soraiban az asztalon lévő cédulák megfelelő sorrendjét adja meg! (A megadott táblázat sorainak a száma lehet több, kevesebb vagy ugyanannyi, mint a felsorolandó esetek száma. Ennek megfelelően hagyja üresen a felesleges mezőket, vagy egészítse ki újabb mezőkkel a táblázatot, ha szükséges!)

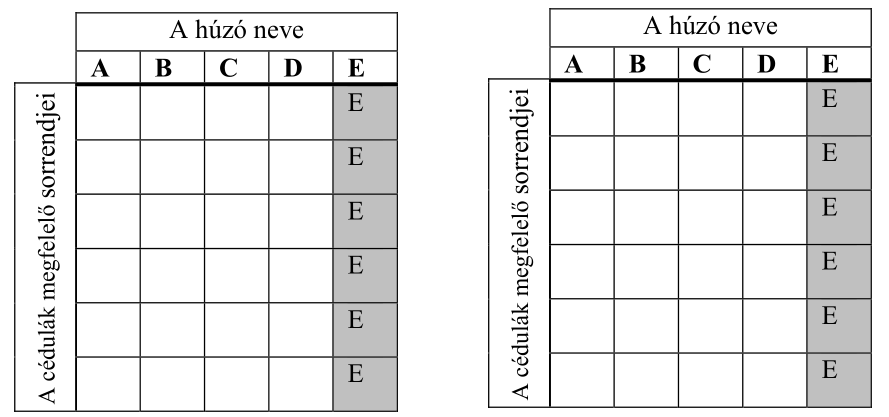
c) Az ajándékok átadása után mind az öten moziba mentek, és a nézőtéren egymás mellett foglaltak helyet. Hány különböző módon kerülhetett erre sor, ha tudjuk, hogy a két fiú nem ült egymás mellett?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba