a) Mely valós számok elégítik ki az alábbi egyenlőtlenséget?

$(x-1)^3-(x+1)^3>-8 $

b) Az alábbi $ f $ és $ g $ függvényt is a $ [- 3 ; 6] $ intervallumon értelmezzük. $ f (x) = \sqrt{ x + 3 } $ és $ g(x) = -0,5x + 2,5 $. Ábrázolja közös koordinátarendszerben az $ f $ és a $ g $ függvényt a $ [- 3 ; 6] $ intervallumon! Igazolja számolással, hogy a két grafikon metszéspontjának mindkét koordinátája egész szám!

c) Oldja meg az alábbi egyenlőtlenséget a valós számok halmazán!

$ 0,5x + \sqrt{ x + 3 } \le 2,5 $

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Hány olyan tízjegyű pozitív egész szám van, amelynek minden számjegye a $ \{0 ; 8\} $ halmaz eleme?

b) Írja fel a 45-nek azt a legkisebb pozitív többszörösét, amely csak a 0 és a 8-as számjegyeket tartalmazza!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az $ ABCDEFGH $ téglatest A csúcsból induló élei: $ AB=12 $; $ AD=6 $; $ AE=8 $. Jelölje a $ HG $ él felezőpontját $ P $.

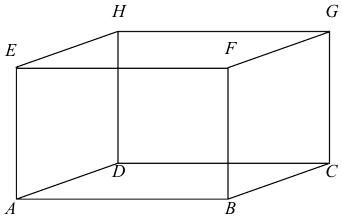
a) Számítsa ki az $ ABCDP $ gúla felszínét!

b) Mekkora szöget zár be az $ ABCDP $ gúla $ ABP $ lapjának síkja az $ ABCD $ lap síkjával?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy felmérés során megkérdeztek 640 családot a családban élő gyermekek számáról, illetve azok neméről. A felmérés eredményét az alábbi táblázat mutatja:

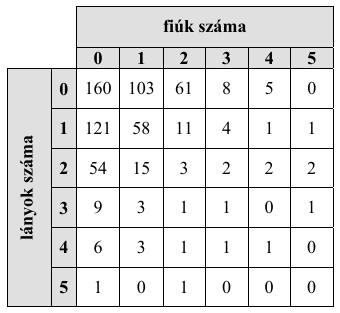
(Tehát pl. a gyermektelen családoknak a száma 160, és 15 olyan család volt a megkér- dezettek között, amelyben 1 fiú és 2 lány van.)

a) Hány fiúgyermek van összesen a megkérdezett családokban?

b) A felmérésben szereplő legalább kétgyermekes családokban mennyi a leggyakoribb leányszám?

c) A családsegítő szolgálat a megkérdezett családok közül a legalább négy gyermeket nevelőket külön támogatja. Az alábbi táblázat kitöltésével készítsen gyakorisági táblázatot a külön támogatásban részesülő családokban lévő gyermekek számáról!

Hány családot és összesen hány gyermeket támogat a családsegítő szolgálat?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba