Feladatbank keresés

Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium

Látogatók

Összes:

6 970 709

Mai:

2 421

Honlapok

SULINET Matematika

Oktatási Hivatal

Versenyvizsga portál

Matematika Portálok

Berzsenyi Dániel Gimnázium

Óbudai Árpád Gimnázium

Szent István Gimnázium

Békásmegyeri Veres Péter Gimnázium

Első lap
1
Utolso lap

Találatok száma: 4 (listázott találatok: 1 ... 4)

1. találat: ARANYD 2016/2017 Kezdő I. kategória és II. kategória 1. forduló 1. feladat
Témakör: *Számelmélet (számjegy) (Azonosító: AD_20162017_k1k1f1f, AD_20162017_k2k1f1f )

Melyik 15-nek az a legkisebb pozitív többszöröse, amelynek tízes számrendszerbeli alakja csak a 0 és a 7 számjegyeket tartalmazza?

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

2. találat: ARANYD 2016/2017 Kezdő I. kategória és II. kategória 1. forduló 2. feladat
Témakör: *Algebra (útvonal) (Azonosító: AD_20162017_k1k1f2f, AD_20162017_k2k1f2f )

Hányféleképpen olvasható ki Arany Dániel neve az alábbi ábrából, ha az olvasás során csak jobbra és lefelé haladhatunk?

A	R	A	N
R	A	N	Y
A	N	Y	D	Á	N	I	E	L
			Á	N	I	E	L
			N	I	E	L
			I	E	L
			E	L
			L

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

3. találat: ARANYD 2016/2017 Kezdő I. kategória és II. kategória 1. forduló 3. feladat
Témakör: *Kombinatorika (logika) (Azonosító: AD_20162017_k1k1f3f, AD_20162017_k2k1f3f )

Egy osztályba 15 gyerek jár, és az osztálynak 4 társasjátéka van. Minden gyerek legalább 1 játékkal szeret játszani. Bizonyítsuk be, hogy az alábbi állítások között biztosan van igaz!

A. Legalább 3 olyan gyerek van, aki pontosan 4 játékkal szeret játszani.

B. Legalább 4 olyan gyerek van, aki pontosan 3 játékkal szeret játszani.

C. Legalább 5 olyan gyerek van, aki pontosan 2 játékkal szeret játszani.

D. Legalább 6 olyan gyerek van, aki pontosan 1 játékkal szeret játszani.

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

4. találat: ARANYD 2016/2017 Kezdő I. kategória és II. kategória 1. forduló 4. feladat
Témakör: *Geometria (terület) (Azonosító: AD_20162017_k1k1f4f, AD_20162017_k2k1f4f )

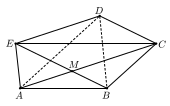
Az ábrán látható ABCDE konvex ötszög minden átlója párhuzamos azzal az oldallal, amelyikkel nincs közös végpontja. Legyen az AC és a BE átlók metszéspontja M. Bizonyítsd be, hogy az ABC háromszög területe egyenl˝o az EMC háromszög területével!