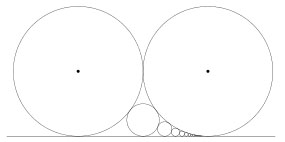
Két egységsugarú kör – k₀ és k₁ – érinti egymást és egy egyenest. Berajzoltuk azt a legnagyobb k₂ kört, amelyik a k₀ -t és k₁ -et is, és az egyenest is érinti. Majd berajzoltuk a k₁ , k₂ és az egyenes közé rajzolható legnagyobb k₃ kört. És így folytatjuk tovább. Mekkora a k₂₀₁₇ sugara?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Adott egy ötelemű halmaz, a halmaz elemei különböző egész számok. Vegyük minden részhalmaza esetén a részhalmaz elemeinek összegét. Maximum hányszor fordulhat elő a 7 az ilyen összegek között?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Oldja meg a következő egyenletet a valós számok halmazán!

$\dfrac{3x+3}{\sqrt{x}}=4+\dfrac{x+1}{\sqrt{x^2-x+1}}$

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba