11.óra - Két alakzat együttes szimmetriái

M.: Táblai eszközeink:

Táblai eszközeink átlátszóak legyenek! Lehet írásvetítős megoldás, én ezeket Á-4-es pausz papírra rajzoltam vastag fekete filccel – tökéletesen használható. Ez esetben mágnes, vagy gyurmaragasztó is szükséges a rögzítéshez. Ugyanilyen ábrákkal rendelkezzenek a gyerekek, családi gyufaskatulya méretben, másolópapíron. Célszerű ezek elkészítését házi feladatként adni 2-3 órával korábban. (Azért kettővel, hogy a hiánypótlás is meglegyen, mert fontos, hogy minden gyerek a maga kezével dolgozva jusson tapasztalatokhoz.)

F1.: Egy-egy alakzatpárt fogunk vizsgálni az előkészített 4 közül. Hányféleképpen választható ki egy pár?  Sorold is fel azokat!
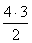= 6 pár választható ki:
- a) szög – egyenes,
- b)  szög – kör,
- c)  szög – piskóta,
- d)  egyenes – kör,
- e)  egyenes – piskóta,
- f) kör – piskóta
F2.:Helyezd el az a) párt úgy, hogy a két alakzat együtt is szimmetrikus legyen, majd tedd ugyanezt a többi párral is! Melyik esetben hány megoldást találtál? Fogalmazd meg, mire kell figyelni az elhelyezéskor!
a) A szögfelező illeszkedik az egyenesre , vagy merőleges az egyenesre;
b) A körközéppont illeszkedik a szögfelezőre;
c) A szögfelezőre illeszkedik a piskóta egyik tengelye;
d) A kör bárhová tehető: a közös tengely átmegy a körközépponton, és merőleges, vagy illeszkedik az egyenesre. Adott ponton átmenő, adott egyenesre merőleges egyenes pedig mindig létezik.
e) A piskóta egyik tengelye illeszkedik az egyenesre, vagy merőleges rá;
f) A kör középpontja illeszkedik a piskóta egyik tengelyére.

Két tengelyesen szimmetrikus alakzat együttesen is szimmetrikus, ha az egyik alakzat egyik tengelye illeszkedik a másik alakzat valamely tengelyére.

Térjünk vissza a d) vizsgálatához. Kör és egyenes kölcsönös helyzeteit átismételjük, közben felidézzük az elnevezéseket. (érintő, szelő, húr, érintési pont, metszéspont, sugár, átmérő)

K.: Ha a kört érinti az egyenes, akkor mit mondhatunk a tengelyről?
A tengely ekkor is merőleges az egyenesre, és áthalad a középponton, a „többlet”: áthalad az érintési ponton is. Ha ugyanis nem haladna át rajta, akkor az érintési pont képe nem önmaga lenne, hanem tőle különböző MÁSIK ÉRINTÉSI PONT, azaz két közös pont lévén nem érintkezés, hanem metszés esete állna fenn.

Az érintő merőleges az érintési pontba húzott sugárra.

K.: Ha a kört metszi az egyenes, akkor mit mondhatunk a tengelyről?
Mivel ez esetben a metszéspontok egymás tükörképei, ezért a tengely a húrt merőlegesen felezi.
A kör bármely húrjának felezőmerőlegese áthalad a kör középpontján.
M.: Ezek után elvárhatjuk, hogy a kör adott pontjában érintő egyenes szerkesztésére módszert találjanak tanítványaink. Ha megszületett az ötlet, 1-2 érintőt szerkesszünk is meg, de ne sokat, mert unalmas, inkább kössük össze a gyakorlást egy kis problémamegoldással!
Pl.: A szabályos sokszögeket – ha még nem ismerik – mutassuk be a gyerekeknek! Gyengébb osztályban elég a háromszögről beszélnünk, ügyesebbekkel a hatszöget is górcső alá vehetjük. Adjunk definíciót (a szabályos sokszög olyan sokszög, melynek minden oldala és minden szöge egyenlő), majd vizsgáljuk meg a kiválasztott sokszög esetében (a háromszög, vagy a hatszög), hogy az milyen tulajdonságokkal bír. (A háromszögek, majd a sokszögek belső szögösszegét a SZÖGEKről szóló fejezetben, 5. év végén, esetleg 6. év elején, tehát e témakör előtt tárgyal(hat)juk, most ezt felhasználva „lökjük mélyvízbe” a gyerekeket.
F.: Vegyél fel egy 3 cm sugarú kört! Szerkessz olyan szabályos háromszöget (vagy hatszöget), melynek minden oldala érintője a körnek!
M.: Bátran próbáljuk ki gyengébb osztályokban is! Látni fogjuk, hogy többféle ötlettel is előhozakodnak tanítványaink, 3-4 különböző megoldás is születik. Feladtam olyan osztályban, ahol a 75°-os szög szerkesztése nehéz, megtanulandó eljárásnak bizonyult, és a gyerekek szívesen és eredményesen bajlódtak vele.

Előző fejezet    Tartalom