A 2002-2003 tanévi 11-12-es FPI tehetséggondozó szakkör 15. foglalkozása
Kódok
Összeállította Hraskó András és Szőnyi Tamás
1.1
Egy cég 10 szériában gyártott egész kg-os
súlyokat. Az első szériában 1, a másodikban 2, a harmadikban 3, ... a
tizedikben 10 kg-os súlyokat terveztek készíteni. Az azonos szériában készült
egyforma súlyokat ugyanabban a ládában tartják, mind a 10 ládára rá van írva,
hogy hanyadik szériában készült. Az egyik széria hibás lett, példányai egyforma
súlyúak, de ez az érték nem egyezik meg az előre adott értékkel.
a) Egy kijelzős mérleg egyszeri
használatával kell megtalálnunk, hogy mennyivel nehezebbek vagy könnyebbek a
hibás súlyok az előírtnál.
b) Ezután határozzuk meg, hogy melyik súly szériája lett hibás!
Most is csak a kijelzős mérleget használhatjuk, és azt is csak még egyszer.
c) Próbáljuk meg általánosítani előző eredményeinket.
Fontos volt-e, hogy épp 10 széria volt?
Lényeges-e, hogy rendre épp 1, 2, 3, ... 10 kg-osak a súlyok az egyes szériákban?
Fogalmazzuk meg általánosan a feladatot, és adjunk választ az a), b) kérdésekre
az általános esetben is!
d) Módosítunk az eredeti feladaton. Tegyük
fel, hogy mindegyik súly megfelelő tömegű (az egyes szériákban rendre 1, 2, ...
10 kg), de előfordulhat, hogy amikor a ládákat a bennük lévő súlyok növekvő
sorrendjében betolták a raktárba egymás mellé, akkor két szomszédos ládát
felcseréltek. Ezután rakták rájuk sorban a szériaszámokat, amelyek így most
növekvő sorrendben vannak, de lehet, hogy az egyik szomszédos párnál nem a
ládában levő súlyok tömegét jelzik.
Hány méréssel lehet megállapítani, hogy történt-e ilyen tévesztés?
Megoldás:
a) Rakjunk föl a mérlegre mindegyik súlyból
egyet-egyet, és nézzük meg mennyivel tér el a tömeg 1+2+3+4+5+6+7+8+9+10=55
kg-tól.
b) Rakjunk a mérlegre az első szériából 1,
a másodikból 2, ..., a tizedikből 10 súlyt és nézzük meg mennyivel tér el a
tömeg 1·1 + 2·2 + 3·3 + 4·4
+ 5·5 + 6·6 + 7·7 + 8·8
+ 9·9 + 10·10 kg-tól. Az eltérés és az előző
mérésben kapott hiba hányadosa épp a hibás súlyok szériaszáma.
Nem ez az egyetlen jó megoldás. Az a lényeg, hogy mindegyik szériából különböző számú
súlyt tegyünk föl a mérlegre.
c) Ha n széria van, és az egyes
szériákban a súlyok tervezett tömege rendre x1, x2,
x3, .., xn, de az egyik széria hibás, akkor
x1 + x2 + x2 + ... + xn,
illetve x1 + 2x2 + 3x2 +
... + nxn lekérdezése megoldja a két feladatot.
d) I. mego. A b)-ben adott mérés
most is jó lesz. Ha pld a 4. és 5. szériát felcseréljük, akkor a várt és a
tényleges tömeg különbsége:
4·4 + 5·5
4·5 + 5·4
4·(-1)+5·1 = 1.
d) II. mego. Tegyünk fel az elsőtől kezdve minden
második szériából egyet-egyet a mérlegre!
Az 1+3+5+7+9 összeget várjuk eredménynek. Ha volt csere, akkor nem ennyit kapunk.
Tanári kérdés: a fenti két
megoldás között van-e olyan, amely akkor is jó, ha nem szomszédos ládákat
cseréltek föl? És olyan, ami akkor is kimutatja a tévedést, ha nem volt csere,
de az egyik széria hibás? (Az I. megoldás mindkettőre jó.)
5.1
Számrontó Rezsőnek két módszere van egy szám elrontására. Vagy egy számjegyet tetszőlegesen
megváltoztat (pld. 5437→5487), vagy két számjegyet kicserél (pld.
5437→3457). Egyszer véletlenül az asztalon hagytam egy cetlit a
másológép négyjegyű belépési számával. Rezső ezt meglátta és rögtön átjavította
1323-ra. Szerencsére észrevettem, és visszajavítottam az eredeti számra. De,
amikor legközelebb lehetősége adódott Rezső megint elrontotta a cetlin lévő
számot, így most 1213 van ráírva. Mi lehet a másológép belépési száma?
Dobos Sándor
Megoldás:
négy megoldás is van: 1223, 1313, 1233, 1123.
5.5
A térbeli sakktáblán a bástya a tábla
oldaléleivel párhuzamosan tud lépni. Legfeljebb hány bástya helyezhető el a
táblán úgy, hogy semelyik kettő se üsse egymást, ha a tábla
a) 3×3-as?
b) 8×8-as?
Megoldás:
a) 9-nél több bástya nem helyezhető el, mert
a 9 oszlop mindegyikében legfeljebb egy lehet. 9 elhelyezhető, az alábbi ábrán
a kocka 3 rétege külön-külön látható, a korongok a bástyákat jelzik. Egy táblán
belül semelyik két bástya sincs ugyanabban a sorban vagy oszlopban, a különböző
táblákon lévő bástyák soha sincsenek a tábla ugyanazon mezőjén.
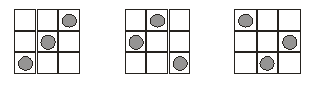
b) 64 a megoldás. A konstrukció az előzőhöz
hasonló, a főátló nyolc bástyáját ciklikusan fölfelé toljuk.
5.8
a) Az 1, 2, 3, ... 16 számok közül kell
kitalálni egyet barkochba kérdésekkel. Legalább hány kérdésre van szükség?
b) És ha a kérdéseket előre le kell írni,
azaz a következő kérdés nem függhet az előzőre kapott választól?
Megoldás:
a) Egy-egy kérdés a szóbajövő számok
halmazát két részhalmazra bontja: azokra, amelyekre igen a válasz (ha az a szám
a gondolt szám) és azokra, amelyekre nem a válasz. "Rossz esetben"
olyan választ kapunk, amely azt mutatja, hogy a nagyobb, pontosabban a nem
kisebb részhalmazban van a gondolt szám. Ezért, ha biztosra megyünk nem
tehetünk jobbat, minthogy kérdéseinkkel megfelezzük a lehetőségeket. 4 kérdés
kell a kitaláláshoz, és ennyi elég is.
b) Házi feladatnak maradt
1.2
Egy cég 5 szériában gyártott súlyokat. Az
egyes szériákon belül mindegyik súly egyforma tömegű, de nem ismert, hogy
mekkorák. Az éppen távol levő cégvezető meg szeretné tudni, hogy milyen tömegű
súlyokat gyártottak. Ezért egy mérési űrlapot küld egyik alkalmazottjának, majd
annak kell elvégeznie a méréseket, és visszaküldeni az eredményekkel kitöltött
űrlapot.
Legalább hány
mérést kell elvégezni, és mik legyenek ezek a mérések (hogyan töltse ki a
cégvezető az 1., 2., ..., 5. oszlopokat), ha várható, hogy (legfeljebb) egyszer
az alkalmazott hibás értéket ír be a "Mért tömeg" rovatba?
Az űrlap így néz ki:
|
Hány súly legyen az egyes szériákból a
mérlegen? |
Mért tömeg |
|
1. széria |
2. széria |
3. széria |
4. széria |
5. széria |
(kg) |
1. mérés |
|
|
|
|
|
|
2. mérés |
|
|
|
|
|
|
3. mérés |
|
|
|
|
|
|
4. mérés |
|
|
|
|
|
|
5. mérés |
|
|
|
|
|
|
6. mérés |
|
|
|
|
|
|
7. mérés |
|
|
|
|
|
|
8. mérés |
|
|
|
|
|
|
9. mérés |
|
|
|
|
|
|
10. mérés |
|
|
|
|
|
|
11. mérés |
|
|
|
|
|
|
I. megoldás (Mindent háromszor)
15 mérés elég. Sorra vesszük a szériákat, mindig csak egy súlyt veszünk ki belőlük és
azt a súlyt háromszor is megmérjük. Így a jó eredményt mindegyik szériánál
legalább kétszer is megkapja a cégvezető, így tudni fogja a helyes
eredményeket.
Megjegyzés: ez a módszer jó, de nem optimális.
II. megoldás(Az I. megoldás javítása)
Az előző módszert alkalmazom, de csak kétszer mérek meg minden súlyt, majd kizárólag azt
teszem fel harmadszorra is, amelynél két különböző eredményt kaptam. Így 11
méréssel oldom meg a feladatot.
Megjegyzés: ez a módszer nem szabályos, mert nincs
lehetőség a cégvezetőnek menet közben beleszólni, hogy melyiket mérje meg még
egyszer az alkalmazott.
III. megoldás (Újabb javítás)
Én is csak kétszer mérek meg minden súlyt, végül pedig mindegyik szériából egyet-egyet
tetetek fel a mérlegre,
így 11 méréssel oldom meg a feladatot. Ha az egyesével mért súlyok egyikénél a két mérés
nem ugyanazt az eredményt adta, akkor tudhatjuk, hogy az utolsó mérés jó, így
annak eredményéből, és a másik négy súly tömegéből meghatározható a
bizonytalan eredmény is.
IV. megoldás
7 méréssel
oldom meg a feladatot. Az első öt mérésben csak egy-egy súlyt teszünk a
mérlegre, az elsőben az első, a másodikban a második, ... az ötödikben az
ötödik szériából. A hatodik mérésben öt súlyt, mindegyik szériából egyet-egyet
teszünk a mérlegre. A hetedik mérésben 15 súlyt, az első szériából egyet, a másodikból
kettőt, ... az ötödikből ötöt teszünk a mérlegre. Ha a hatodik vagy a hetedik
mérés eredménye összhangban van az első öt mérés eredményével, akkor az első öt
mérés mindegyikének jó az eredménye, tudjuk a tömegeket. Ha a hatodik és a
hetedik mérés eredménye sincs összhangban az első öt mérés eredményével, akkor
az első öt között van a hiba. Most az 1.1 feladat a) és b) része megoldásának alapján
készen vagyunk.
Hat mérés nem elég. Ennek igazolására később térünk vissza.
Házi feladat (5.8-hoz)
Egy mérési
tervhez meg kell adni az előírt mérések számát - a továbbiakban ezt n
jelöli - továbbá nemnegatív egész számokkal kell kitölteni az űrlap 1., 2., 3.,
4., 5. oszlopait. Jelölje az így kapott számtáblázat i-edik sorának (i
= 1, 2, ..., n) j-edik oszlopába (j = 1, 2, 3, 4, 5) írt
számot aij (aij természetes szám). Tehát aij
-vel jelölöm az i-edik mérésnél a j-edik szériából vett
súlyok számát. Határozzunk meg az aij számokkal kapcsolatos
olyan algebrai feltételt, amely azzal ekvivalens, hogy a mérésekből
meghatározhatók a súlyok (feltéve, hogy legfeljebb egy hibás az eredmények
közül).
4.1
(Pálvölgyi Dömötör példája, Bergengóc példatár 2. 237. fel.)
A budapesti telefonszámok hétjegyűek. Sokszor előfordul, hogy valaki két szomszédos számot
felcserél, ezért téves a
hívása. Keress minél egyszerűbb eljárást arra, hogy a hétjegyű számok végére
még egy ellenőrző számot téve, a központ számcsere (két szomszédos
felcserélése) esetén jelezni tudja, hogy a szám téves, és ne kapcsoljon!
5.2
Egy hajó és utasai, összesen 100 fő, Ungabunga
szigetén az emberevők fogságába esett. Tudják, hogy másnap reggel a kannibálok
leültetik őket egymás mögé, és mindegyikük fejére egy-egy piros vagy kék sapkát
húznak. Mindenki csak az összes előtte ülő ember fején lévő sapkát fogja látni,
a sajátját és a mögötte ülőkét nem. A leghátsó embertől kezdve sorban mindenki
hangosan mondhat majd egy színt: pirosat vagy kéket. A végén azt engedik szabadon,
aki saját sapkája színét mondta, aki nem találta el, azt bizony megeszik. A
kannibálok szigorúak, ha bárki mást tesz, minthogy a lehető legegyszerűbben
kimondja a "piros" vagy a "kék" szót, akkor senkinek sem kegyelmeznek.
A foglyoknak
még egy esélye van. Most este még összebeszélhetnek. Szeretnék, hogy minél
többen megszabaduljanak. Hány fogoly tud biztosan megmenekülni?
Könnyítés: oldjuk meg előbb a feladatot abban az
esetben, ha tudjuk, hogy összesen pontosan
a2) két;
a10) tíz;
piros sapka van a 100 között!
5.3
Gondoljuk végig az 5.2 feladatot kettő
helyett három színnel! Minden rab fején háromféle sapka lehet, és mindenki
háromféle színt is mondhat.
