a) Péter és Pál szendvicset és ásványvizet vásárolt a büfében. Péter két szendvicset és két ásványvizet vett 740 Ft-ért, Pál pedig három szendvicset és egy ásványvizet 890 Ft-ért. Mennyibe kerül egy szendvics, és mennyibe kerül egy ásványvíz?

b) Oldja meg az alábbi egyenletet a valós számok halmazán!

$ 1-x=\sqrt{x+5} $

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az $ ABCD $derékszögű trapézban az $ A $ és a $ D $ csúcsnál van derékszög. Az $ AB $ alap 11 cm, a $ BC $ szár 12 cm, a $ CD $ alap 5 cm hosszú.

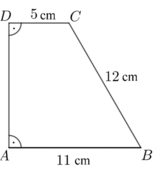
a) Igazolja, hogy a trapéz $ B $ csúcsánál lévő szög nagysága $ 60^\circ $, és számítsa ki a trapéz területét!

b) Számítsa ki az $ ABC $ háromszög $ C $ csúcsánál lévő szögét!

xxxképxxx

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Egy számtani sorozat negyedik tagja 4, tizenhatodik tagja –2. Számítsa ki a sorozat első 120 tagjának az összegét!

b) Adott egy szakasz két végpontja: $ A(0; 4) $ és $ B(2; 3) $. Írja fel az $ AB $ szakasz felezőmerőlegesének egyenletét!

c) Egy elsőfokú függvény a 0-hoz 4-et, a 2-höz 3-at rendel. Írja fel a függvény hozzárendelési szabályát!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Anna dominókészletében a dominókövek egyik oldala egy vonallal két részre van osztva. Az egyes részeken a pöttyök száma 0, 1, 2, 3, 4, 5 vagy 6 lehet. A készletben minden lehetséges pöttyözésű dominóból pontosan egy darab van. Az ábrán a 2-6-os (6-2-es) dominó látható.

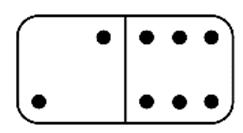
a) Hány olyan dominó van a készletben, amelyen a két részen lévő pöttyök számának szorzata prímszám?

A játékban két dominó akkor csatlakozhat egymáshoz, ha a két érintkező részen ugyanannyi pötty van. (Lásd az ábrát.)

Anna egy lapra elhelyezte dominókészletének azt a hat dominóját, amelyek mindkét részén van legalább 1, de legfeljebb 3 pötty. Ezután összekötötte azokat a dominókat, amelyeket a játékban csatlakoztatni lehetne egymáshoz. Az alábbi ábra a hat dominót és az összekötő vonalakat mutatja, de csak két részen adtuk meg a pöttyöket.

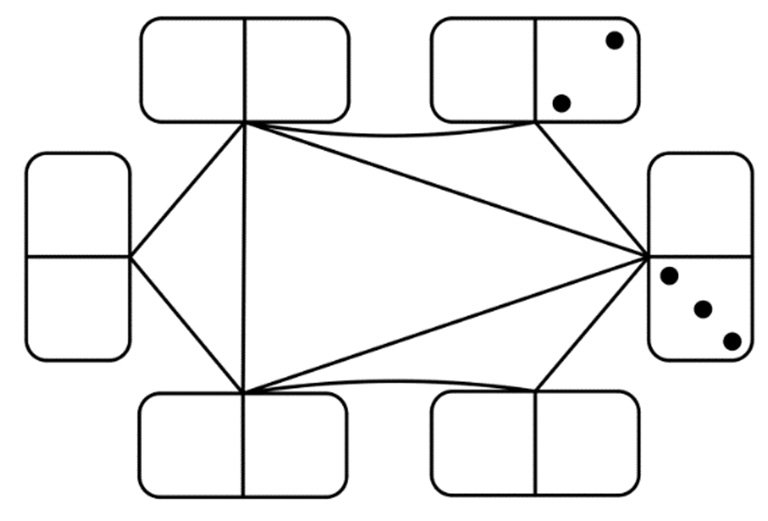
b) Rajzolja be a tíz üres részre a hiányzó pöttyöket az összekötésnek megfelelően! Anna a teljes 28 darabos készletből kihúzta a 2-6-os dominót. Ezután véletlenszerűen kihúz még egy dominót.

c) Számítsa ki annak a valószínűségét, hogy a másodiknak kihúzott dominót csatlakoztatni tudja az elsőhöz!

Egy játékbemutatóra Anna és Balázs 1800 dominót szeretne felállítani a földre úgy, hogy a legelsőt meglökve az összes dominó sorban eldőljön. Anna egyedül 6 óra alatt, Balázs pedig 9 óra alatt építené meg a dominóláncot.

d) Ha Anna és Balázs – tartva a saját tempójukat – együtt dolgozna, akkor hány óra alatt végeznének az 1800 dominó felállításával?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy jégkrémgyártó üzem fagylalttölcséreket rendel. A csonkakúp alakú fagylalttölcsér belső méretei: felső átmérő 7 cm, alsó átmérő 4 cm, magasság 8 cm.

a) Számítsa ki, hogy a tölcsérbe legfeljebb hány cm3 jégkrém fér el, ha a jégkrém – a csomagolás miatt – csak a felső perem síkjáig érhet!

Ennek a tölcsérnek létezik olyan változata is, amelynek a belső felületét vékony csokoládéréteggel vonják be. 1 kg csokoládé kb. $ 0,7 m^2 $ felület bevonásához elegendő.

b) Számítsa ki, hogy hány kilogramm csokoládéra van szükség 1000 darab tölcsér belső felületének bevonásához! Válaszát egész kilogrammra kerekítve adja meg!

Egy fagylaltozóban hatféle ízű fagylalt kapható: vanília, csokoládé, puncs, eper, málna és dió. Andrea olyan háromgombócos fagylaltot szeretne venni tölcsérbe, amely kétféle ízű fagylaltból áll.

c) Hányféle különböző háromgombócos fagylaltot kérhet, ha számít a gombócok sorrendje is? (Például a dió-dió-vanília más kérésnek számít, mint a dió-vanília-dió.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy 30 fős osztályban felmérést készítettek a diákok internetezési szokásairól. Az egyik kérdés az volt, hogy naponta átlagosan ki hány órát használja az internetet a szabadidejében. A válaszok alapján az itt látható kördiagram készült.

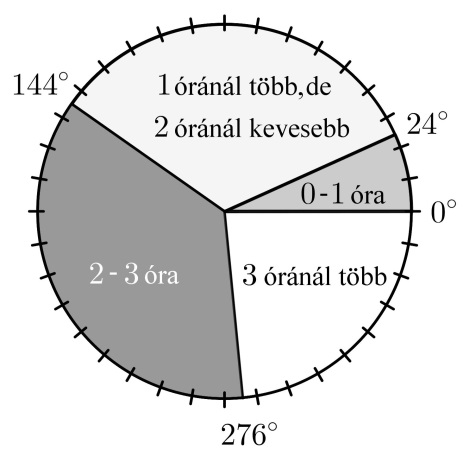
a) Hány olyan diák van az osztályban, aki naponta legalább 2 órát használja az internetet a szabadidejében?

Egy másik kérdés az volt, hogy a mobiltelefon, a laptop, illetve a táblagép (tablet) közül melyiket használják internetezésre. A mobiltelefont mind a 30-an, a laptopot 24-en, a táblagépet 16-an jelölték meg. A felmérésből az is kiderült, hogy a mobiltelefon, a laptop és a táblagép közül pontosan kétféle eszközt 14 diák használ.

b) Hányan használják mind a háromféle eszközt internetezésre?

A vezeték nélküli hálózati kapcsolatot létrehozó egységek (wifi routerek) $ 3\% $-a 2 éven belül meghibásodik (ezt úgy tekinthetjük, hogy 0,03 annak a valószínűsége, hogy egy készülék meghibásodik 2 év alatt). A meghibásodott eszközt garanciálisan kicserélik. Az iskola 20 ilyen eszközt vásárolt.

c) Mennyi a valószínűsége annak, hogy 2 év alatt legfeljebb egy hibásodik meg a vásárolt eszközök közül?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba