Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
Látogatók
Összes:
7 328 081 Mai:
5 146 18-97-14-82.crawl.commoncrawl.org
(IP: 18.97.14.82) HonlapokSULINET Matematika Oktatási Hivatal Versenyvizsga portál Matematika Portálok |
1. találat: Matematika középszintű érettségi, 2015. május, I. rész, 1. feladat Témakör: *Algebra (szorzattá alakítás, algebrai tört) (Azonosító: mmk_201505_1r01f ) Egyszerűsítse az $\dfrac{a^3+a^2}{a+1}$ törtet, ha $a\neq -1$. Témakör: *Számelmélet (oszthatóság, oszthatósági szabály) (Azonosító: mmk_201505_1r02f ) Milyen számjegy állhat az X helyén, ha a négyjegyű $\overline{361X}$ szám 6-tal osztható? Témakör: *Logika (negáció) (Azonosító: mmk_201505_1r03f ) „Minden szekrény barna.” Válassza ki az alábbiak közül annak a mondatnak a betűjelét, amelyik tagadása a fenti kijelentésnek! A) Van olyan szekrény, amelyik nem barna. B) Nincs barna szekrény. C) Van olyan szekrény, amelyik barna. D) Pontosan egy szekrény barna. Témakör: *Algebra (Azonosító: mmk_201505_1r04f ) Az $x^2+bx-10=0$ másodfokú egyenlet diszkriminánsa 49. Számítsa ki b értékét! Számítását részletezze! Témakör: *Geometria ( logika, térgeometria) (Azonosító: mmk_201505_1r05f ) Adja meg az alábbi állítások logikai értékét (igaz vagy hamis)! A) Minden paralelogramma tengelyesen szimmetrikus négyszög. B) A kocka testátlója $ 45^\circ$-os szöget zár be az alaplappal. C) A szabályos tizenhétszögben az egyik csúcsból kiinduló összes átló a tizenhétszöget 15 háromszögre bontja. Témakör: *Függvények (szélsőérték) (Azonosító: mmk_201505_1r06f ) Adja meg a valós számok halmazán értelmezett $x \mapsto (x-2)^2$ függvény minimumának helyét és értékét! Témakör: *Statisztika (Azonosító: mmk_201505_1r07f ) Egy mérőállomáson az egyik év júliusának tizenhárom egymást követő napján az alábbi csapadékértékeket mérték (milliméterben): 2; 26; 8; 1; 6; 1; 21; 10; 22; 49; 5; 25; 9. Adja meg az adatsor terjedelmét és mediánját! Témakör: *Kombinatorika ( gráfok) (Azonosító: mmk_201505_1r08f ) Rajzoljon olyan hatpontú gráfot, amelyben a pontok fokszáma: 0; 1; 2; 2; 3; 4. Témakör: *Algebra ( mértani sorozat) (Azonosító: mmk_201505_1r09f ) Egy bomlási folyamatban a radioaktív részecskék száma kezdetben $ 6 \cdot 10^{23}$, amely érték percenként az előző érték századrészére csökken. Számítsa ki a radioaktív részecskék számát 10 perc elteltével! Témakör: *koordinátageometria (Azonosító: mmk_201505_1r10f ) Egy kör egyenlete: $(x+3)^2+(y-4)^2=25$. Adja meg a kör középpontjának koordinátáit és a kör átmérőjének hosszát! 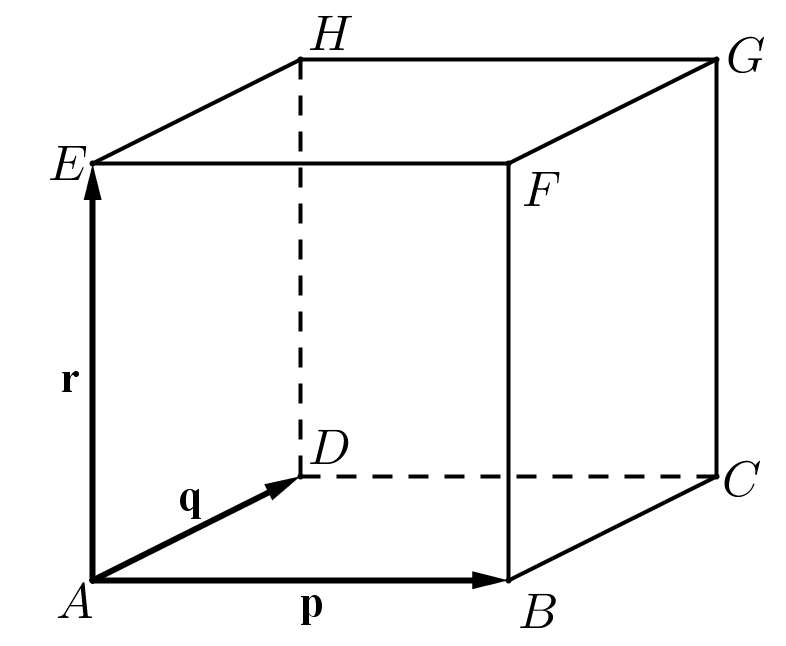Témakör: *Geometria ( vektor, térgeometria) (Azonosító: mmk_201505_1r11f ) Az ábrán látható kocka A csúcsából kiinduló élvektorai $\overrightarrow{AB}=\textbf{p}; \overrightarrow{AD}=\textbf{q}; \overrightarrow{AE}=\textbf{r} $. Fejezze ki p, q és r segítségével a $\overrightarrow{GC}$, az $\overrightarrow{AG}$, és az $\overrightarrow{FH}$ vektorokat!
Témakör: *Valószínűségszámítás ( számelmélet, oszthatóság) (Azonosító: mmk_201505_1r12f ) Két különböző színű szabályos dobókockával egyszerre dobunk. Adja meg annak a valószínűségét, hogy a dobott számok szorzata prímszám lesz! Megoldását részletezze!
|
KeresésHonlapokKözépiskolai Matematikai és Fizikai Lapok Wolfram Alpha Art of Problem Solving Kvant IMO |
|||||||||||||||||
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
| |||||||||||||||||||
| |||||||||||||||||||
|
Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium
|
|
1082 Budapest, Horváth Mihály tér 8. OM azonosító: 035277 |
Joomla template: szsnjm4-001 (c) Szoldatics József 2011/2024
www.szolda.hu
www.szolda.hu