1. találat: Matematika középszintű érettségi, 2010. október, II. rész, 13. feladat
Témakör: *Algebra (Azonosító: mmk_201010_2r13f )
Oldja meg a valós számok halmazán a következő egyenlőtlenségeket!
a) $ x-\dfrac{x-1} 2 > \dfrac{x-3} 4 - \dfrac{x-2} 3 $
b) $-3x^2-1\le -4 $
Mindkét esetben ábrázolja a megoldáshalmazt számegyenesen!
*Geometria (Azonosító: mmk_201010_2r14f )
Az iskolatejet gúla alakú, impregnált papírból készült dobozba csomagolják. (Lásd az alábbi ábrát, ahol $ CA = CB = CD $ .)
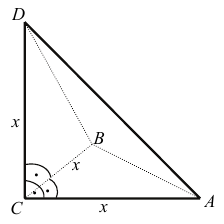
A dobozba 2,88 dl tej fér.
a) Számítsa ki a gúla éleinek hosszát! Válaszát egész $ cm $-ben adja meg!
b) Mekkora a papírdoboz felszíne? Válaszát $ cm^2 $-ben, egészre kerekítve adja meg!
*Kombinatorika (Azonosító: mmk_201010_2r15f )
Egy kockajátékban egy menet abból áll, hogy szabályos dobókockával kétszer dobunk egymás után. Egy dobás 1 pontot ér, ha négyest, vagy ötöst dobunk, egyébként a dobásért nem jár pont. A menetet úgy pontozzák, hogy a két dobásért járó pontszámot összeadják.
a) Mennyi annak a valószínűsége, hogy egy menetben 1 pontot szerzünk, és azt az első dobásért kapjuk?
b) Minek nagyobb a valószínűsége,
- annak, hogy egy menetben szerzünk pontot, vagy
- annak, hogy egy menetben nem szerzünk pontot?
*Algebra (Azonosító: mmk_201010_2r16f )
a) Egy számtani sorozat első tagja -7, a nyolcadik tagja 14. Adja meg n lehetséges értékeit, ha a sorozat első n tagjának összege legfeljebb 660.
b) Egy mértani sorozat első tagja ugyancsak -7, a negyedik tagja -189. Mekkora az n, ha az első n tag összege -68 887?
*Geometria (Azonosító: mmk_201010_2r17f )
Az ábrán egy ejtőernyős klub kitűzője látható. (Az egyik körív középpontja a szabályos háromszög A csúcsa, a másik körív középpontja az A csúccsal szemközti oldal felezőpontja.) Ezt a lapot fogják tartományonként színesre festeni.
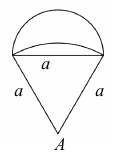
a) A Számítsa ki egyenként mindhárom tartomány területét, ha a = 2,5 cm ! Számításait legalább két tizedesjegy pontossággal végezze, és az így kapott eredményt egy tizedesjegyre kerekítve adja meg!
b) Hányféle módon festhető színesre a kitűző, ha minden tartományt a piros, sárga, zöld és kék színek valamelyikére festenek a következő két feltétel együttes figyelembe vételével:
(1) szomszédos tartományok nem lehetnek azonos színűek;
(2) piros és sárga színű tartomány nem lehet egymás mellett. (Szomszédos tartományoknak van közös határvonala.)
*Kombinatorika (Azonosító: mmk_201010_2r18f )
Megkérdeztek 25 családot arról, hogy hány forintot költöttek az elmúlt hónapban friss gyümölcsre. A felmérés eredményét mutatja az alábbi táblázat:
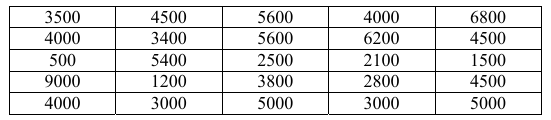
(Az adatokat tekintsük pontos értékeknek!)
a) Hány forintot költöttek átlagosan ezek a családok friss gyümölcs vásárlására az elmúlt hónapban?
b) Ossza 1000 Ft terjedelmű osztályokba a fenti értékeket, kezdve a 0-1000 Ft, 1001-2000 Ft stb. osztályokkal, és ábrázolja ezeknek az osztályoknak a gyakoriságát oszlopdiagramon!
c) Az 500 Ft és a 9000 Ft kiugró értékek. Mennyi a megmaradt adatok átlaga, ha ezeket a kiugró értékeket elhagyjuk az adatok közül? Hány százalékos változást jelent ez az eredeti átlaghoz képest, és milyen irányú ez a változás? Mennyi az így keletkezett új adatsor terjedelme?
(Azátlagot forintra, a százaléklábat két tizedesjegyre kerekítve adja meg!)
d) Az eredeti mintát a vizsgálatot végző cég két új család megfelelő adatával bővítette. Az egyik az eredeti átlagnál 1000 Ft-tal többet, a másik ugyanennyivel kevesebbet költött havonta friss gyümölcsre. Mutassa meg számítással, hogy így az átlag nem változott!


