Sorolja fel a 2010-nek mindazokat a pozitív osztóit, amelyek prímszámok!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Oldja meg az egyenletet a valós számok halmazán!

$ x^2-25=0$

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az alábbi táblázat egy 7 fős csoport tagjainak cm-ben mért magasságait tartalmazza. Mekkora a csoport átlagmagassága? A csoport melyik tagjának a magassága van legközelebb az átlagmagassághoz?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az $ \mathbb{R}^+ \to \mathbb{R}, x \to  3 +\log_2 x $ függvény az alább megadott függvények közül melyikkel azonos?

A: $ \mathbb{R}^+ \to \mathbb{R}, x \to  3\log_2 x $

B: $ \mathbb{R}^+ \to \mathbb{R}, x \to  \log_2 {8x} $

C: $ \mathbb{R}^+ \to \mathbb{R}, x \to  \log_2 {3x} $

D: $ \mathbb{R}^+ \to \mathbb{R}, x \to  \log_2 x^3 $

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Annának kedden 5 órája van, mégpedig matematika (M), német (N), testnevelés (T), angol (A) és biológia (B). Tudjuk, hogy a matematikaórát testnevelés követi, és az utolsó óra német. Írja le Anna keddi órarendjének összes lehetőségét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy egyenlő szárú háromszög alapja 5 cm, a szára 6 cm hosszú. Hány fokosak a háromszög alapon fekvő szögei? A szögek nagyságát egész fokra kerekítve adja meg! Válaszát indokolja!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

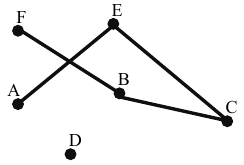
Az ábrán látható hatpontú gráfba rajzoljon be 2 élt úgy, hogy a kapott gráf minden csúcsából 2 él induljon ki! A berajzolt éleket két végpontjukkal adja meg!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az alábbi kilenc szám közül egyet véletlenszerűen kiválasztva, mekkora annak a valószínűsége, hogy a kiválasztott szám nem negatív? -3,5; -5; 6; 8,4; 0; -2,5; 4; 12; -11.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Oldja meg a valós számok halmazán a $ \sin x = 0 $ egyenletet, ha $ -2 \le x \le 2\pi $?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Döntse el az alábbi négy állításról, hogy melyik igaz, illetve hamis!

A: Van olyan derékszögű háromszög, amelyben az egyik hegyesszög szinusza $ \dfrac{1}{ 2} $ .

B: Ha egy háromszög egyik hegyesszögének szinusza $ \dfrac{1}{ 2} $ , akkor a háromszög derékszögű.

C: A derékszögű háromszögnek van olyan szöge, amelynek nincs tangense.

D: A derékszögű háromszögek bármelyik szögének értelmezzük a koszinuszát.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A héten az ötös lottón a következő számokat húzták ki: 10, 21, 22, 53 és 87. Kata elújságolta Sárának, hogy a héten egy két találatos szelvénye volt. Sára nem ismeri Kata szelvényét, és arra tippel, hogy Kata a 10-est és az 53-ast találta el. Mekkora annak a valószínűsége, hogy Sára tippje helyes? Válaszát indokolja!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy 17 fős csoport matematika témazáró dolgozatának értékelésekor a tanár a következő információkat közölte: Mind a 17 dolgozatot az 1-es, a 2-es, a 3-as, a 4-es és az 5-ös jegyek valamelyikével osztályozta. A jegyek mediánja 4, módusza 4, terjedelme 4 és az átlaga (két tizedes jegyre kerekítve) 3,41. Döntse el, hogy az alábbi állítások közül melyik igaz, illetve hamis!

A: A dolgozatoknak több mint a fele jobb hármasnál.

B: Nincs hármasnál rosszabb dolgozat.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba