Kinga a következő tanítási napra hat házi feladatot kapott, három kötelezőt és három szorgalmit. Egy-egy kötelező házi feladatot kapott matematikából, angolból és magyarból, ezeket biztosan elkészíti. Szorgalmi házi feladatot biológiából, németből és történelemből kapott, ezeket nem feltétlenül csinálja meg: lehet, hogy mind a hármat elkészíti, lehet, hogy csak kettőt vagy egyet, de az is lehet, hogy egyet sem készít el.

a) Összesen hányféle különböző sorrendben készítheti el Kinga a házi feladatait? (Két esetet különbözőnek tekintünk, ha vagy nem ugyanazokat a házi feladatokat, vagy ugyanazokat a házi feladatokat, de más sorrendben oldja meg.)

Kinga matematika-házifeladata ez volt: "500 különböző pozitív egész szám átlaga 1000. Legfeljebb mekkora lehet a számok közül a legnagyobb?"

b) Adja meg Kinga matematika-házifeladatának megoldását!

Kinga, Linda, Misi és Nándi elvállalta, hogy az alacsonyabb évfolyamok tanulói közül hét diákot rendszeresen korrepetálni fog. Az egyénenként vállalt tanulók számát egy megbeszélésen döntik el.

c) Hány különböző módon állapodhatnak meg abban, hogy melyikük hány tanulót korrepetáljon, ha mindegyikük vállal legalább egy tanulót? (Két megállapodást különbözőnek tekintünk, ha legalább egyikük nem ugyanannyi tanulót korrepetál a két megállapodás szerint.) 

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Határozza meg az alábbi két állítás logikai értékét (igaz vagy hamis)! Válaszait indokolja!

I. Ha egy trapéznak 2-2 szöge egyenlő, akkor a trapéz húrtrapéz.

II. Ha egy háromszögben $ a=b $, akkor $ \sin 3\alpha= \sin 3\beta $. (A háromszög oldalai a, b és c, a velük szemközti szögek rendre $ \alpha $, $ \beta $ és $ \gamma $.)

b) Fogalmazza meg a II. állítás megfordítását, és a megfordított állításról is döntse el, hogy igaz vagy hamis! Válaszát indokolja!

Egy matematika-vizsgafeladatban három állítás logikai értékét kell meghatározni (igaz vagy hamis). Három helyes válasz esetén 2, két helyes válasz esetén 1, kettőnél kevesebb helyes válasz esetén 0 pontot kap a vizsgázó. Béla tanult egy keveset, de bizonytalan a tudása: mindegyik kérdésnél 0,6 valószínűséggel találja el a helyes választ.

c) Számítsa ki annak a négy eseménynek a valószínűségét, hogy Béla sikeres tippjeinek száma 3, 2, 1, illetve 0, és határozza meg Béla pontszámának várható értékét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A római katonák az úgynevezett taxillus-szal játszottak "kockajátékot". (A taxillus a keske vagy a juh térdkalácsából faragott csontocska; ld. a képen.)

Dobás után egy taxillus négy különböző oldalára eshetett. Jelölje ezt a négy különböző helyzetet A, B, C és D. Az egyes dobáskimenetelek nem voltak egyformán valószínűek: az A, illetve a B helyzet egyaránt $ \dfrac{4}{10} $, a C, illetve a D helyzet pedig egyaránt $ \dfrac{1}{10} $ valószínűséggel következett be. A rómaiak általában négy taxillust dobtak fel egyszerre. A Venus-dobás volt az egyik legértékesebb, ekkor a négy csontocska mindegyike más-más oldalára esett.

a) Mennyi a Venus-dobás valószínűsége?

b) Az alábbi két esemény közül melyiknek nagyobb a valószínűsége?

I. Négy feldobott taxillus között lesz olyan, amelyik C helyzetben érkezik le.

II. Négy feldobott taxillus között pontosan egy érkezik le az A helyzetben.

Thalész, a hét görög bölcs egyike, egy nevezetes, neki tulajdonított mérés során egy folyóban lévő sziget AB hoszszát a folyóparton maradva határozta meg.

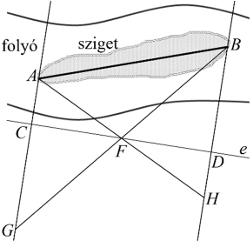
Először felvett egy e egyenest a parton. Ezen az e egyenesen megkereste azt a C, illetve D pontot, amelyekben a CA, illetve a DB irány merőleges az e egyenesre. Ezután a CD szakasz F felezőpontját is megjelölte egy jelzőkaróval. Ezt követően az AC egyenesen haladva megjelölte azt a G pontot, amelyre B, F és G egy egyenesre illeszkedik; és hasonlóan az AF és BD egyenesek H metszéspontját is megjelölte. Thalész azt állította, hogy a sziget hossza a GH távolsággal egyezik meg.

c) Igazolja Thalész állításának helyességét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az $ ABCDEFGH $ négyzetes oszlop $ AE $, $ BF $, $ CG $, $ DH $ élei merőlegesek az $ ABCD $ alaplapra. Az $ A $ csúcsból kiinduló három él hossza $ AB = AD = 8$ egység, $AE=15$ egység.

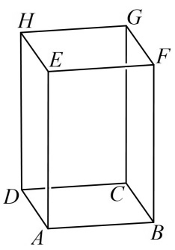
a) Számítsa ki az $ \overline{EF }$ és $ \overline{AH }$ vektorok skaláris szorzatát!

A négyzetes oszlop köré egy $P $ csúcspontú forgáskúpot illesztünk úgy, hogy az $ A $, $ B $, $ C $, $ D $ csúcsok a kúp alaplapjára, az $ E $, $ F $, $ G $, $ H $ csúcsok pedig a kúp palástjára illeszkedjenek. (A kúp és a négyzetes oszlop tengelye egybeesik.) A kúp magassága 45 egység.

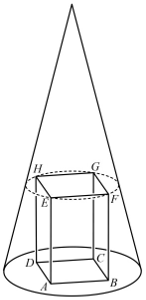
b) Számítsa ki a kúp felszínét!

c) Hány olyan derékszögű háromszög van, amelynek egyik befogója $ 15 $ egység hosszú, és a másik két oldala is egész szám hosszúságú? (Az egybevágó háromszögeket nem tekintjük különbözőknek.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Határozza meg a $ p > 0 $ paraméter értékét úgy, hogy $ \int\limits_0^p \left(3x^2-24x+20\right)\ dx=0$ teljesüljön!

b) Határozza meg az $ a, b, c $ valós paraméterek értékét úgy, hogy az $ f (x)=ax^3+bx^2+cx+28\ (x\in\mathbb{R}) $ függvénynek $ x=2 $-ben zérushelye, $ x=-4 $-ben lokális maximumhelye, $ x=-1 $-ben pedig inflexiós pontja legyen!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba