a) Határozza meg a c számjegy lehetséges értékeit, ha tudjuk, hogy $ \overline{1c28} $ nem osztható 6-tal, $ \overline{93c6} $ nem osztható 36-tal, $ \overline{c3c5} $ pedig nem osztható 15-tel! ($ \overline{pqrs} $ azt a négyjegyű számot jelöli, melynek első számjegye p, további számjegyei pedig rendre q, r és s.)

b) Igazolja, hogy nincs olyan n pozitív egész szám, amelyre $ 4^n+6n-1 $ osztható 8-cal!

c) Igazolja (teljes indukcióval vagy más módszerrel), hogy $ 4^n+6n-1 $ minden n pozitív egész szám esetén osztható 9-cel!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy fémlemezből készült, forgáshenger alakú hordóban 200 liter víz fér el.

a) Mekkora területű fémlemez kell a 80 cm magas, felül nyitott hordó elkészítéséhez, ha a gyártása során 12%-nyi hulladék keletkezik?

Egy kisvállalkozásnál több különböző méretben is gyártanak 200 literes, forgáshenger alakú lemezhordókat.

b) Mekkora annak a 200 liter térfogatú, felül nyitott forgáshengernek a sugara és magassága, amelynek a legkisebb a felszíne?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy baktériumtenyészet szaporodását laboratóriumi körülmények között vizsgálják. Az első órában 4 mikrocellát fertőznek meg baktériumokkal. A második órában a baktériumok szaporodni kezdenek, így további 3 cella fertőződik meg. A megfigyelés szerint ezután „szabályszerűvé” válik a baktériumok szaporodása: minden órában annyi új fertőzött cella keletkezik, ahány korábban összesen volt. (A harmadik órában 4 + 3 = 7 új fertőzött mikrocella keletkezik, a negyedik órában 14, és így tovább.)

a) Ha a baktériumok szaporodásához továbbra is biztosítanák a megfelelő körülményeket, akkor az összes fertőzött mikrocella száma hányadik órában haladná meg a tízmilliót?

A biológiaórán egy kezdetben tízmilliós baktériumhalmaznak a környezethez való alkalmazkodását modellezik a tanulók. Egy szabályos dobókockával dobnak, és ha a dobás eredménye 1, 2 vagy 3, akkor egymillió baktérium elpusztul. Ha a dobás eredménye 4 vagy 5, akkor nem történik semmi. Ha a dobás eredménye 6, akkor újabb egymillió baktérium keletkezik. A dobást többször egymás után megismétlik.

b) Számítsa ki annak a valószínűségét, hogy hét dobás után a baktériumok száma legfeljebb ötmillió lesz!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Ha egy háromszög szabályos, akkor a körülírt körének középpontja megegyezik a beírt körének középpontjával. Fogalmazza meg a fenti (igaz) állítás megfordítását, és igazolja, hogy a megfordított állítás is igaz!

Az egységnyi oldalú ABC szabályos háromszög minden csúcsánál behúztunk egy-egy szögharmadoló egyenest, így az ábrán látható PQR szabályos háromszöget kaptuk.

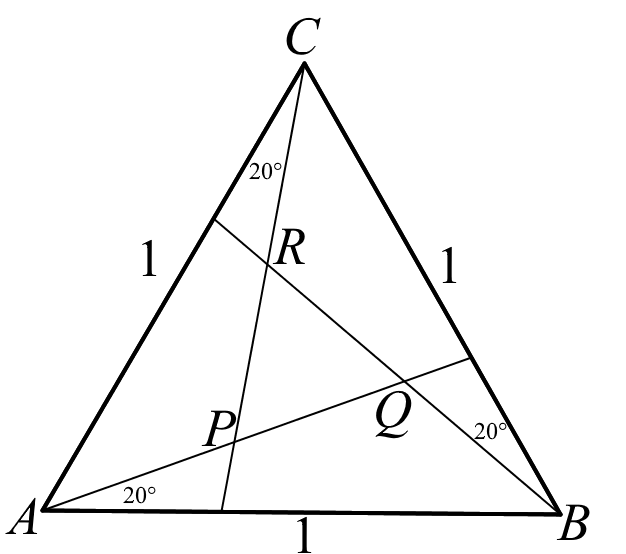
b) Számítsa ki a PQR háromszög oldalának hosszát!

A piros, kék, zöld és sárga színek közül három szín felhasználásával úgy színezzük ki az ábrán látható ABQ, BCQ, CQR, ACP és PQR háromszögek belsejét, hogy a közös határszakasszal rendelkező háromszögek különböző színűek legyenek. (Egy-egy háromszög színezéséhez csak egyegy színt használunk.)

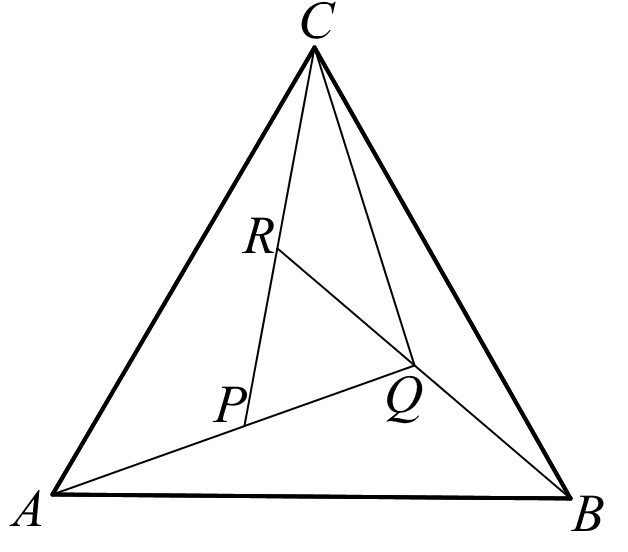
c) Összesen hány különböző színezés lehetséges?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy pár kesztyű árát először p százalékkal csökkentették, majd a csökkentett ár p + 4,5 százalékával tovább mérsékelték. A kétszeri árcsökkentés után a kesztyű 18,6%-kal olcsóbb lett, mint az árcsökkentések előtt volt.

a) Határozza meg a két árcsökkentés százalékos értékét!

Egy fiókban három pár kesztyű van összekeveredve: az egyik pár fekete, a másik szürke, a harmadik piros. (A három pár kesztyű csak a színében különböző.) A fiókból egyesével elkezdjük kihúzni a kesztyűket úgy, hogy húzás előtt nem nézzük meg a kesztyű színét, és a kihúzott kesztyűket nem tesszük vissza a fiókba. Addig folytatjuk a húzást, amíg lesz két azonos színű kesztyűnk.

b) Határozza meg annak a hat eseménynek a valószínűségét, hogy ehhez 1, 2, 3, 4, 5, illetve 6 kesztyű kihúzására lesz szükség, majd számítsa ki a húzások számának várható értékét!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba