Jelölje $ A $ az $ \dfrac{x+4}{x-3}\le0 $ egyenlőtlenség egész megoldásainak a halmazát, $ B $ pedig az$| x + 3| < 4 $ egyenlőtlenség egész megoldásainak a halmazát. Elemei felsorolásával adja meg az $ A \cap B $, az $ A \setminus B $és az $ A \cup B $ halmazt!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

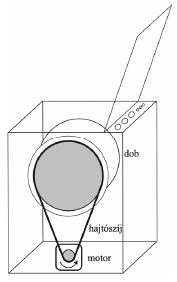
Az ábrán egy mosógép vázlatos rajza látható. A kisebb, 1 cm sugarú kerék a motor tengelyéhez kapcsolódik, és egy hajtószíj segítségével forgatja meg a mosógép dobjához rögzített, 20 cm sugarú kereket, amitől a dob és benne a ruhák forognak mosás közben. A két kerék tengelye párhuzamos, a tengelyek távolsága 46 cm. (A hajtószíj a tengelyekre merőleges síkban van.) Milyen hosszú a feszes hajtószíj?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Tekintsük a következő, egyszerű gráfokra vonatkozó állítást:

Ha a gráf minden pontjának fokszáma legalább 2, akkor a gráf biztosan összefüggő.

a) Döntse el, hogy igaz vagy hamis az állítás! Válaszát indokolja!

b) Fogalmazza meg az állítás megfordítását! Döntse el, hogy igaz vagy hamis az állítás megfordítása! Válaszát indokolja!

Tekintsük a következő halmazokat: $ P = \{\text{összefüggő gráfok}\} $, $ Q = \{\text{egyszerű gráfok}\} $, $ R = \{\text{kört tartalmazó gráfok}\} $.

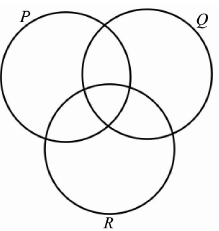
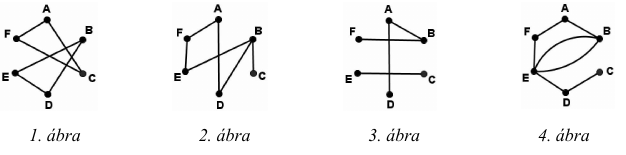
c)Helyezze el az alábbi gráfok ábrájának sorszámát a fenti halmazábrában a megfelelő helyre!

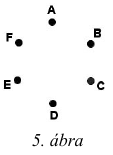
d) Rajzoljon egy 6 pontú fagráfot az 5. ábrára, és helyezze el ennek a sorszámát is a fenti halmazábrában a megfelelő helyre!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

a) Egy bank olyan hitelkonstrukciót ajánl, amelyben napi kamatlábat számolnak úgy, hogy az adott hitelre megállapított éves kamatlábat 365-tel elosztják. Egy adott évben a hitelfelvételt követően minden napra kiszámolják a napi kamat értékét, majd ezeket december 31-én összeadják és csak ekkor tőkésítik (azaz a felvett hitel értékéhez adják). Ez a bank egy adott évben évi $ 8\% $-os kamatlábat állapított meg. Éva abban az évben a március 1-jén felvett 40 000 Ft után október 1-jén újabb 40 000 Ft hitelt vett fel. A két kölcsön felvétele után mennyi kamatot tőkésít a bank december 31-én? (A hitelfelvétel napján és az év utolsó napján is számítanak napi kamatot.)

b) Ádám is vett fel hiteleket ettől a banktól évi $ 8\% $-os kamatos kamatra. Az egyik év január 1-jén éppen 1 000 000 Ft tartozása volt. Több hitelt nem vett fel, és attól kezdve 10 éven keresztül minden év végén befizette az azonos összegű törlesztőrészletet. (A törlesztőrészlet összegét a bank már az éves kamattal megnövelt tartozásból vonja le.) Mekkora volt ez a törlesztőrészlet, ha Ádám a 10 befizetés után teljesen visszafizette a felvett hitelt? Válaszát ezer forintra kerekítve adja meg!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba