Kinga 10. születésnapja óta kap havi zsebpénzt a szüleitől. Az első összeget a 10. születésnapján adták a szülők, és minden hónapban 50 Ft-tal többet adnak, mint az azt megelőző hónapban. Egy bizonyos hónapban, mikor éppen 1850 Ft volt a havi zsebpénze, összeadta az addig kapott összes zsebpénzét. Az összeg 35100 Ft lett. Mennyi volt Kinga induló zsebpénze, és hány hónap telt el a 10. születésnapja óta?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Az ENSZ 1996-ban megjelent táblázatának egy részlete a nyolc legnagyobb népességszámú ország népességi adatait tartalmazza 1988-ban, és egy népesedésdinamikai modell előrejelzése alapján 2050-ben.

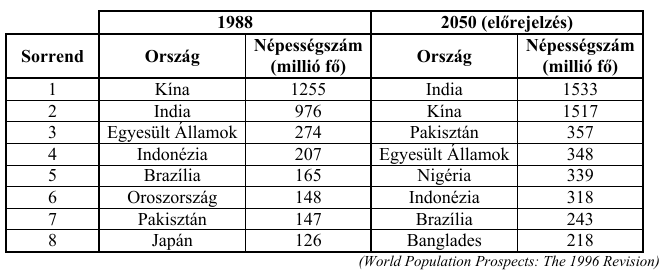
Feltételezzük, hogy Pakisztán lakossága 1988 és 2050 között minden évben ugyanannyi százalékkal nő, mint amennyi százalékkal az előző évben növekedett.

a) Ezzel a feltételezéssel élve - millió főre kerekítve - hány lakosa lesz Pakisztánnak 2020-ban? (Az évi százalékos növekedés két tizedesjegyre kerekített értékével számoljon!)

b) A táblázat mindkét oszlopában szereplő országok népességi adataira vonatkozóan mennyivel változik az átlagos lakosságszám és a medián 1988 és 2050 között? (Válaszát millió főben, két tizedesjegyre kerekítve adja meg.)

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy 32 fős érettségiző osztály tanulói három különböző táncot mutatnak be a szalagavató bálon. Az alábbi táblázat az egyes táncokban fellépő diákok számát mutatja nemenkénti bontásban.

Van 2 olyan lány, aki mindhárom táncban fellép, ugyanakkor nincs olyan fiú az osztályban, aki egynél több produkcióban részt venne.

a) A lányok közül kettőt véletlenszerűen kiválasztva, mennyi annak a valószínűsége, hogy mindketten táncolnak a kán-kánban?

b) Az osztály tanulói közül egyet véletlenszerűen kiválasztva, mennyi a valószínűsége annak, hogy az illető pontosan két táncban szerepel?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Oldja meg a következő egyenletrendszert, ha $ x $ és $ y $ valós számok, továbbá $ x > 0, x \ne 1 \text{ és } y > 0 , y \ne1$.

$ \begin{cases} \log_x y + \log_y x = 2 \\ \sin (2x + 3y) + \sin(4x + y) = 1 \end{cases} $

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba