Az $ A_1C_0C_1 $ derékszögű háromszögben az $ A_1 $ csúcsnál $ 30^\circ $-os szög van, az $ A_1C_0 $ befogó hossza 1, az $ A_1C_1 $ átfogó felezőpontja $ A_2 $. Az $ A_2C_1 $ szakasz "fölé" az $ A_1C_0 C_1 $ háromszöghöz hasonló $ A_2 C_1C_2 $ derékszögű háromszöget rajzoljuk az ábra szerint.

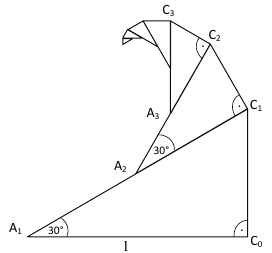
Az $ A_2C_2 $ átfogó felezőpontja $ A_3 $. Az $ A_3C_2 $ szakasz "fölé" az $ A_2C_1 C_2 $ háromszöghöz hasonló $ A_3 C_2C_3 $ derékszögű háromszöget rajzoljuk. Ez az eljárás tovább folytatható.

a) Számítsa ki az így nyerhető végtelen sok derékszögű háromszög területének összegét (az összeg első tagja az $ A_1C_0C_1 $ háromszög területe)!

b) Igazolja, hogy a $ C_0C_1C_2...C_n $ töröttvonal hossza minden pozitív egész n-re kisebb, mint $ 1,4 $.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Adott a síkbeli derékszögű koordináta-rendszerben az $ x^{ 2} + y^ 2 + 6 x + 4 y - 3 = 0 $ egyenletű kör. Ebbe a körbe szabályos háromszöget írunk, amelynek egyik csúcsa $ A(1; –2) $.

a) Számítsa ki a szabályos háromszög másik két csúcsának koordinátáit! Pontos értékekkel számoljon!

b) Véletlenszerűen kiválasztjuk az adott kör egy belső pontját. Mekkora a valószínűsége annak, hogy a kiválasztott pont a tekintett szabályos háromszögnek is belső pontja? Válaszát két tizedes jegyre kerekítve adja meg!

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

A nyomda egy plakátot 14 400 példányban állít elő. A költségeket csak a nyomtatáshoz felhasznált nyomólemezek (klisék) darabszámának változtatásával tudják befolyásolni. Egy nyomólemez 2500 Ft-ba kerül, és a nyomólemezek mindegyikével óránként 100 plakát készül el. A nyomólemezek árán felül, a lemezek számától függetlenül, minden nyomtatásra fordított munkaóra további 40 000 Ft költséget jelent a nyomdának. A ráfordított idő és az erre az időre jutó költség egyenesen arányos.

a) Mennyi a nyomólemezek árának és a nyomtatásra fordított munkaórák miatt fellépő költségnek az összege, ha a 14 400 plakát kinyomtatásához 16 nyomólemezt használnak?

b) A 14 400 plakát kinyomtatását a nyomda a legkisebb költséggel akarja megoldani. Hány nyomólemezt kell ekkor használnia? Mennyi ebben az esetben a nyomólemezekre és a ráfordított munkaidőre jutó költségek összege?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Egy fából készült négyzetes oszlop minden élének hossza centiméterben mérve 2-nél nagyobb egész szám. A négyzetes oszlop minden lapját befestettük pirosra, majd a lapokkal párhuzamosan 1 cm élű kis kockára vágtuk. A kis kockák közül 28 lett olyan, amelynek pontosan két lapja piros. Mekkora lehetett a négyzetes oszlop térfogata?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Hány $ (x; y) $ rendezett valós számpár megoldása van az alábbi egyenletrendszernek, ha $ x $ és $ y $ is a$ [ 0 ; 2\pi ] $ zárt intervallum elemei?

$\begin{cases} \sin x \cdot \cos y = 0 \\ \sin x + \sin^2 y = \dfrac 1 4  \end{cases} $

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba