


|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 7 | 4 | 2 | 5 | 8 | 2 | |
| + | 8 | 4 | 9 | 4 | 3 | 0 |
| 1 | 2 | 1 | 2 | 0 | 1 | 2 |
A karneváli mulatság minden évben álarcosbállal ér véget. Az idén 15 lány még éjfél elôtt távozott, a táncra emiatt kétszer annyi fiú maradt, mint ahány lány. Az első valcer alatt 45 fiú lesántult - vagy KöMaL-határidő volt -, így aztán minden hadrafogható fiúra 5 leányzó maradt. Hányan voltak ott kezdetben?
A nagyhírű Serpenyős gimnázium egyik matadorának kidőlt a tintásüvege és a dolgozatban kapott másodfokú egyenletből csak x2 + ...+12 = 0 maradt. Mintha az elsőfokú tag együtthatója egész szám lett volna és valami - vagy valaki - azt súgta neki, hogy a gyökök is egészek. Ha tényleg ez a helyzet, akkor hány másodfokú egyenletet kell végignéznie?
A Gauss-eliminációval sikeresen eltávolított paca alól újabb feladat bukkant elô: "Egy n-edfokú ($n\ge0$) $P(x)=a_nx^n+a_{n-1}x^{n-1}+\ldots+a_1x+a_0$ polinom súlyának az $s=n+|a_0|+|a_1|+\ldots+|a_n|$ számot nevezzük. Hány olyan egész együtthatós polinom adható meg, amelynek a súlya 3"?
A városi krónikák följegyezték, hogy a költségvetés hiánya évről évre az alábbi különös törvényszerűség szerint alakul: ha az alapítástól számított n-edik évben f(n) jelöli a hiányt, akkor f(1) = 1 és minden pozitív egészre f(2n) = 2f(n)+1. Mennyi a hiány az alapítástól számított 1024-edik évben?
A Serpenyős gimnázium diákjainak 80 százaléka kitűnő matematikus, 75 százalékuk éltornász, 70 százalékuk pedig nagyon szépen énekel. Legalább hány százalékuk tünteti ki magát mindhárom fenti tantárgyból?
Matekland telefonszámának titkos elôkódjáról tudjuk, hogy ez a legnagyobb olyan tízes számrendszerben felírt négyjegyû szám, amely az alábbi tulajdonságokkal rendelkezik:
- a számnak és a palindromjának az összege 7216;
- a számjegyek összege 17;
- a két szélső számjegy eltérése legfeljebb 4.
Mi volt a kód?
Fülöpke már gimnazista, de az óvodában töltött évek nem múltak el fölötte nyomtalanul: dolgozatírás közben például elkérte Eufrozina kalkulátorát és - ő tudja hogy - átprogramozta a billentyûzetét, úgyhogy az most a következő elrendezés szerint működik: 0→0; 1→1; 2→4; 3→7; 4→2; 5→5; 6→8; 7→3; 8→6; 9→9. Ha tehát Eufrozina pl. a 7-es billentyűt nyomja meg, akkor a gép 3-mal számol. Eufrozina gyanútlanul bebillentyűzött két számot, összeszorozta őket és 1996-ot kapott eredményül. Nem tetszett neki a dolog, mert háromjegyű számot várt. Melyiket?
Matekland városának falai egy szabályos sokszöget zárnak körül, melynek belső szöge fokokban mérve egész szám. Hány különböző oldalszámú ilyen sokszög van?
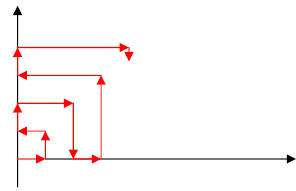
Egy különösen nehéz KöMaL feladaton töprengve Titusz sétálgatni kezd. A sebessége állandó, 1 méter percenként - ennyire töpreng - az útvonala pedig az ábrán látható: az első percben 1 métert andalog jobbra, aztán befordul - ennyire okos -, aztán balra...
Hol lesz a 2005. perc - ennyire nehéz a feladat - leteltével? Válaszul a helyzete koordinátáinak az összegét adjátok meg.
Egy régi fóliánson találták a következő feladatot: a, b és c egész számok, melyekre a + b + c = 9000, továbbá $a\cdot\log_{200}5+b\cdot\log_{200}2=c$. Mennyi b értéke?
Matekland központi bankjában a páncélszekrény legfeljebb négyjegyű titkos kódját a fôpénztáros minden este átállítja: az új kódot a régiből készíti el úgy, hogy annak háromszorosában elhagyja a legelső számjegyet. Egy elvetemült pénztáros valamelyik éjjel megtudta, hogy az aznapi kombináció nem tartalmaz páratlan számjegyet. Másnap éjjel egy őr kiszagolta, hogy az aznapi kód egyik jegye sem osztható 3-mal. A rákövetkező éjjel Enyves, a hírhedt besurranó tolvaj megpróbálta kinyitni a páncélszekrényt; néhány sikertelen kisérlet után arra jutott, hogy az aznapi kód jegyei kivétel nélkül oszthatók kell legyenek 3-mal. Másnap reggel Enyves kihallgatta a pénztáros és az őr beszélgetését és megtudta mindazt, amit ők. Éjszaka aztán növekvő sorrendben próbálta ki a megmaradt lehetőségeket és legutoljára sikerült kinyitnia a páncélszekrényt. Mi volt a kód aznap este?
A város főterén egy háromszög alakú emlékmű épült - számokból. A háromszöget a 0, 1, 2, 3, 4, számok szegélyezik az ábra szerint, a belsejében pedig minden szám az alatta lévő kettő összege. Az n-nel kezdődő sorban álló számok összegét jelöljük f(n)-nel. Mi a maradék, ha f(100)-at 100-zal osztjuk?
| 4 | 7 | 8 | 7 | 4 | ||||
| 3 | 4 | 4 | 3 | |||||
| 2 | 2 | 2 | ||||||
| 1 | 1 | |||||||
| 0 |
Matekland sütődéjében messze földön híres mandulás sütemények készülnek. Egy kerekes puszedli elkészítése három fázisban történik: az első kemencében 6 percig sül, a másodikban 12 percig, végül a harmadikban18 percig. A puszedlis kerék először az első kemencében sül 18 percig, azután a másodikban 12 percig, végül a harmadikban 6 percig. A kemencék minden nap leállnak valamennyi idôre: az első legalább 2 órára, a második legalább 5 órára, a harmadik pedig legalább 1 órára. Hányféleképpen lehet megadni a nemnegatív egészekből álló ( kp , pk ) számpárt úgy, hogy egyetlen nap alatt meg lehessen sütni kp darab kerekes puszedit és pk darab puszedlis kereket?
Plajbász, az akkurátus építész bevásárlóközpontot tervez a város szélén. A rendelkezésre álló telek a 120 méter oldalú ABCD négyzet. Mateklandban az az előírás, hogy a bevásárlóközpontokat két paralelogramma közös részén kell felépíteni. Plajbász azt javasolja, hogy az egyik paralelogramma 60 méter hosszú szemközti oldalai a négyzet AD és BC oldalain legyenek, másikuk ugyancsak 60 méter hosszú szemközti oldalai pedig a négyzet másik két oldalán, AB-n és CD-n. Legyen Tmax és Tmin az így felépíthetô bevásárlóközpont maximális illetve minimális alapterülete. Mennyi Tmax − Tmin ?
A város parkjában most avatják a kockafejűek szobrát, a nagyhírű Smirgli alkotását. A mester egy 12 egységnyi élű kockában egy olyan síkra, amelyik a kockát szabályos hatszögben metszi, mindkét irányban végtelen hatoldalú egyenes hasábot faragott, amelynek a hatszögmetszet volt az alaplapja. Amikor végzett, lesmirglizte a kilógó részeket és meg is volt a szobor: a kocka és a hasáb közös része. Mennyi a térfogata?
Eufrozina és Fülöpke azóta kibékültek és a büfében kártyáznak: a játék a hagyományos Fekete Leves. A ravasz Fülöpkénél három lap maradt, egy kőr, egy káró és egy treff, Eufrozinának még négy lapja van, minden színbôl egy-egy. Fülöpke következik, húz egy lapot Eufrozinától és ha ezzel lesz két egyfoma színű ( a francia kártyában négy "szín" van) lapja, azokat lerakhatja, ha nem, akkor a kezében lévő négy lappal játszik tovább. Most Eufrozina jön, aki Fülöpke lapjai közül húz egyet hasonló feltételekkel és így tovább. A játékot az nyeri, aki valamennyi lapját le tudja rakni. Hány százalék a valószínűsége, hogy Fülöpke nyer?
|
|
Bejelentkezés cikkíróknak |