1. találat: ARANYD 2019/2020 Haladó II. kategória 1. forduló 1. feladat
Témakör: *Algebra (Azonosító: AD_20192020_h2k1f1f )
Oldjuk meg az alábbi egyenletet a valós számok halmazán:
$ 4x^2+\dfrac{1}{x^2}-3=4x-\dfrac{2}{x} $
*Kombinatorika (Azonosító: AD_20192020_h2k1f2f )
Dobjunk 5-ször egy szabályos hatoldalú kockával. Dobásainkat írjuk egymás mellé és alkossunk így 5-jegyű számokat. Tekintsük az összes így létrehozható számot. Melyikből van több és miért: azokból a számokból, amelyekben van legalább két azonos számjegy, vagy azokból, amelyekben nincs két szomszédos 6-os számjegy?
*Geometria (Azonosító: AD_20192020_h2k1f3f )
Mutassuk meg, hogy bármely olyan $ABCDEF$ hatszögre, amelynek minden szöge egyenlő, igaz, hogy $AB-DE = EF -BC = CD-FA$. ($AB$, $BC$, $CD$, $DE$, $EF$ és $FA$ a hatszög oldalainak hosszát jelölik.)
*Kombinatorika (Azonosító: AD_20192020_h2k1f4f )
Legyenek $a_n$ és $b_n$ a következő rekurziókkal megadott sorozatok: $a_1 = 1$; $a_{n+1} = 10 \cdot a_n + 1$ ($n \ge 1$) és $b_1 = 1$; $b_{n+1} = 10 \cdot (b_n + 1)$ ($n \ge 1$), továbbá legyen $c_n = b_n - a_n$. Kiszámolva az $s_{2019} = c_1 + c_2 + c_3 + \ldots + c_{2019}$ összeget; $s_{2019}$-ben mennyi a számjegyek összege?
*Számelmélet (Azonosító: AD_20192020_h2k1f5f )
Adott két halmaz: $A = \{1; 3; 5; 7; 9; 11; 13; 15; 17; 19\}$ és $B = \{2; 4; 6; 8; 10; 12; 14; 16; 18; 20\}$. Határozzuk meg azt a legkisebb pozitív egész számot, amely mind az $A$, mind a $B$ halmaz elemei közül pontosan öthöz relatív prím! (Két pozitív egész szám relatív prím, ha legnagyobb közös osztójuk 1.)
*Algebra (Azonosító: AD_20192020_k1k1f1f, AD_20192020_k2k1f1f )
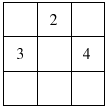
A bűvös négyzet egy olyan négyzet alakú számtáblázat, amelynek minden egyes oszlopában, sorában és átlójában szereplő három szám összege ugyanannyi. Ezt az összeget szokás bűvös összegnek nevezni. Adjuk meg a mellékelt megkezdett ( 3 × 3-as) bűvös négyzet minden lehetséges kitöltését!