Feladatbank keresés

Budapesti Fazekas Mihály Gyakorló Általános Iskola és Gimnázium

Látogatók

Összes:

6 970 921

Mai:

2 633

Honlapok

SULINET Matematika

Oktatási Hivatal

Versenyvizsga portál

Matematika Portálok

Berzsenyi Dániel Gimnázium

Óbudai Árpád Gimnázium

Szent István Gimnázium

Békásmegyeri Veres Péter Gimnázium

Első lap
1
Utolso lap

Találatok száma: 4 (listázott találatok: 1 ... 4)

1. találat: ARANYD 2018/2019 Kezdő I. kategória és II. kategória 1. forduló 1. feladat
Témakör: *Geometria (Azonosító: AD_20182019_k1k1f1f, AD_20182019_k2k1f1f )

Egy trapézról tudjuk, hogy az egyik belső szöge derékszög és két külső szögének aránya 4 : 5. Mekkora lehet a trapéz legkisebb belső szöge?

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

2. találat: ARANYD 2018/2019 Kezdő I. kategória és II. kategória 1. forduló 2. feladat
Témakör: *Algebra (Azonosító: AD_20182019_k1k1f2f, AD_20182019_k2k1f2f )

Egy medencét három csapon keresztül lehet feltölteni. Az 1. és a 2. csap 6 óra alatt, a 2. és 3. csap 4 óra alatt, az 1. és 3. csap 3 óra alatt tölti fel a medencét. Mennyi idő alatt töltik fel a medencét az egyes csapok külön-külön?

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

3. találat: ARANYD 2018/2019 Kezdő I. kategória és II. kategória 1. forduló 3. feladat
Témakör: *Kombinatorika (Azonosító: AD_20182019_k1k1f3f, AD_20182019_k2k1f3f )

Egy diáknak öt egymást követő tanítási napon matematika, angol, biológia és fizika tantárgyakból kell dolgozatot írnia ebben a sorrendben úgy, hogy egy napon legfeljebb két dolgozatot írhat. Hányféleképpen oszthatják el a diák dolgozatait az öt napon? (A dolgozatok egy-egy napon belüli konkrét időpontjai nem számítanak.)

Megtekintés helyben:

Megtekintés új oldalon:

Feladatlapba

4. találat: ARANYD 2018/2019 Kezdő I. kategória és II. kategória 1. forduló 4. feladat
Témakör: *Kombinatorika (Azonosító: AD_20182019_k1k1f4f, AD_20182019_k2k1f4f )

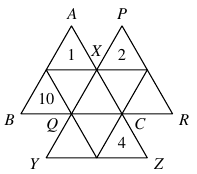
Az ábrán az ABC, PQR és XY Z háromszögek láthatók, amelyek mindegyike 4 kisebb háromszögre van felosztva. A 10 kicsi háromszögbe az 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 számokat kell elhelyezni (mindegyiket egyszer felhasználva) úgy, hogy az ABC, PQR és XY Z háromszögekbe kerülő számok összege egyenlő legyen. Az 1, 2, 4, 10 számok elhelyezése előre adott. Hány különböző módon tölthető ki az ábra? Adjuk meg a megfelelő eseteket!