Egy 8 × 8-as négyzetrács (tábla) 1 × 1-es négyzeteibe (mezőibe) az 1, 2, . . . , k (k 5 64) számokat írjuk valamilyen elrendezésben. Az {1, 2, . . . , k} mezőket együttesen útvonalnak nevezzük. Az útvonal teljes, ha k = 64, tehát az összes mező ki van töltve. Egy zebra lépked a tábla mezőin a következőképpen:

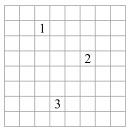
Tegyük fel, hogy a zebra az A mezőn áll. A fel, le, balra, jobbra irányok valamelyikében 2 mezőnyi távolságra mozdulva a táblán a zebra az A mezőből a B mezőbe érkezik, majd az első irányra merőlegesen a B-ből 3 mezőnyi távolságra elmozdulva a táblán a C mezőbe érkezik. Ekkor az A-ból C-be lépés a zebra egy szabályos lépése. Például az ábrán látható 1-es mezőből a 2-es mezőbe lépés egy szabályos zebra-lépés, a 2-es mezőből a 3-as mezőbe lépés egy újabb szabályos zebra-lépés.

Azt mondjuk, hogy az {1, 2, . . . , k} útvonal zebra-útvonal, ha a zebra az 1-es számú mezőből a 2-es számú mezőbe tud lépni szabályos zebra-lépéssel, az i-edik mezőből az i + 1-edikbe tud lépni szabályos zebra-lépéssel minden $ 1 \le i \le k-1$-re. Létezik-e a 8 × 8-as táblán teljes zebra-útvonal?

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Legyen az ABCDE olyan konvex ötszög, melynek oldalaira teljesül, hogy AB + CD = = BC + DE, és az ötszöghöz található olyan k kör, melynek középpontja az AE oldalon van, és a kör az AB, BC, CD és DE oldalakat a P , Q, R, S pontokban érinti. Bizonyítsuk be, hogy az AE és P S egyenesek párhuzamosak.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba

Legyen $a_n=\dfrac{1}{n}+\dfrac{1}{n+1}+\dfrac{1}{n+2}+\ldots+\dfrac{1}{2017}$, ahol $ 1\le i\le 2017,\ n\in \mathbb{N}^+$. Számítsuk ki az $a_1+a_{1}^2+a_{2}^2+ a_{3}^2+ \ldots+ a_{2017}^2 +$ összeg pontos értékét.

Megtekintés helyben:     Megtekintés új oldalon:          Feladatlapba