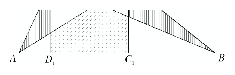
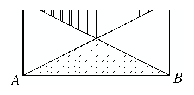
Bizonyítsuk be, hogy az ábrán látható szimmetrikus trapézban a vonalkázott háromszögek területének összege egyenlő a pontozott ötszög területével!

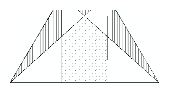
Az ACD és a BCD háromszögek területe egyenként a CDD$_{1}C_{1}$ téglalap területének a fele, hiszen e háromszögek alapja a téglalap CD oldalával, míg ehhez tartozó magasságaik a téglalap másik oldalával egyenlők. Ezért e két háromszög területének az összege a téglalap területével egyenlő.

Ha tehát a CDD$_{1}C_{1}$ téglalap területéből kivonjuk az ACD háromszöggel közös részének a területét, akkor a $D_{1}D_{2}$CC$_{1}$ trapéz területét kapjuk. Ha pedig ebből vonjuk ki a BCD háromszöggel közös részének a területét, akkor a pontozott ötszög területéhez jutunk. Ha viszont az előbbi közös részek területét az ACD és a BCD háromszögek területéből vonjuk ki, akkor a vonalkázott részek területét kapjuk.

2. Megoldás

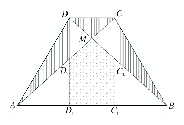
A trapéz szimmetrikus alapjainak felező merőlegesére, ennélfogva a CDD$_{2}C_{2}$ négyszög is szimmetrikus erre.

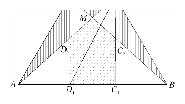
A $C_{2}D_{2}$-nek az alapok felező merőlegesére való szimmetriája miatt a $C_{2}D_{2}$ merőleges a tengelyre, a CDD$_{2}C_{2}$ négyszög tehát téglalap. A téglalapot átlói négy egyenlő területű háromszögre darabolják, így a CDM vonalkázott háromszög területe a pöttyözött ötszög $C_{2}$MD$_{2}$ részháromszögének a területével egyenlő. Most azt fogjuk igazolni, hogy az ADD$_{2}$ vonalkázott háromszög területe a pöttyözött $C_{1}C_{2}D_{2}D_{1}$ téglalap területének a fele. Ebből már a trapéz szimmetrikus voltából következik, hogy a BCC$_{2}$ vonalkázott háromszög -- lévén egybevágó ADD$_{2}$-vel -- területe is a $C_{1}C_{2}D_{2}D_{1}$ területének a fele. Tekintsük az AD$_{1}$CD trapézt. E trapézt átlói négy olyan háromszögre darabolják, amelyek közül a szárakhoz tartozó AD$_{2}D$ és CD$_{1}D_{2}$ háromszögek egyenlő területűek. Ugyanis az ADD$_{1}$ és az ACD$_{1}$ háromszögek területe egyenlő, mivel AD$_{1}$ oldaluk közös, és az ehhez tartozó magasságok is egyenlők, mert CD párhuzamos AD$_{1}$-gyel. Viszont a CD$_{1}D_{2}$ háromszög $D_{1}D_{2}$ oldala a $C_{1}C_{2}D_{1}D_{1}$ téglalapnak is oldala és e közös oldalhoz tartozó magasságaik a $D_{1}D_{2}$ és $C_{1}C$ párhuzamossága miatt egyenlők. Ezzel -- összegezve az eddigieket -- beláttuk a feladatbeli tulajdonságot. Megjegyzések: 1. A téglalap is szimmetrikus trapéz, de a szárak és a $C$ és $D$ csúcsokhoz tartozó magasságok határolta háromszögek egy-egy szakasszá fajulók, ugyanakkor a feladatbeli ötszög is háromszögre módosul. Az ilyen szimmetrikus trapézban is teljesül: a vonalkázott részek területének összege a pontozott rész területe.

2. A feladat általánosítható. Erre az 1. megoldás utal, hiszen a bizonyításban valójában az ABCD négyszög trapéz voltát, és a trapéz által tartalmazott CDD$_{1}C_{1}$ négyszög paralelogrammaságát használtuk fel. Az általánosítás: Bármely trapézban a nem hosszabbik alap csúcsait és a szemköztes oldalt párhuzamosan összekötő szakaszok, továbbá a trapéz átlói a trapézt feldarabolják. E részek közül a két szárhoz és a nem hosszabbik alaphoz tartozó (esetleg elfajuló) háromszögek területének az összege egyenlő az átlók, a nem rövidebb alap, és az alapokat párhuzamosan összekötő szakaszok határolta (esetleg elfajuló) ötszög területével.