Bizonyítsuk be, hogy ha bárhogyan is választunk ki egy egységnyi oldalú négyzet belsejében 19 különböző pontot, akkor van olyan háromszög, amelynek mindhárom csúcsa ezen 19 pont közül való és területe legfeljebb $\frac 1 {18}$ területegység!

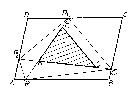
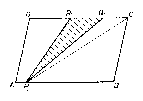
Először belátjuk a következő állítást: Ha egy paralelogramma tartalmaz egy háromszöget, akkor ennek területe nem nagyobb a paralelogramma területének felénél. Legyenek az ABCD paralelogramma által tartalmazott PQR háromszög PR és PQ oldalegyeneseinek a paralelogramma oldalaival való közös pontjai rendre P$_{1}$, R$_{1}$, illetve P$_{2}$, Q$_{1}$ (1. ábra). A P$_{1}$Q$_{1}$R$_{1}$ háromszög tartalmazza háromszögünket, tehát területe nem kisebb a PQR területénél. A P$_{1}$Q$_{1}$R$_{1}$ háromszög területe nem csökken, ha két csúcsának rögzítése mellett a harmadik csúcsát az őt tartalmazó paralelogramma oldal egyik végpontjába helyezzük. Ugyanis, ha például a P$_{1}$R$_{1}$ szakaszt rögzítjük, és Q$_{1}$ a P$_{1}$-et vagy R$_{1}$-et tartalmazó paralelogrammaoldalon van, akkor az oldalnak azt a végpontját választjuk, amelyet Q$_{1}$ elválaszt P$_{1}$-től vagy R$_{1}$-től (2.a ábra). Ha pedig Q$_{1}$ nem az előbbi két paralelogrammaoldal egyikén van, akkor az őt tartalmazó oldal két végpontja közül az egyik nincs közelebb a P$_{1}$R$_{1}$ egyeneshez, mint Q$_{1}$.

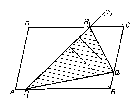
Ily módon tehát a PQR háromszög területe nem nagyobb annak a háromszögnek a területénél, amelynek csúcsai a paralelogramma csúcsai közül valók, ez utóbbi területe pedig a paralelogramma területének a fele. Ezek után eredeti feladatunk megoldására térve, osszuk fel négyzetünket oldalaival párhuzamos egyenesekkel 9 egybevágó négyzetre. Ezek területe $ 1 9$ területegység. A négyzet belsejében elhelyezett 19 pont között van három olyan, amely egy $ 1 9$ területegységnyi négyzeten van, mert ellenkező esetben legfeljebb $ 9\cdot 2=18$ pont volna csak az eredeti négyzet belsejében. Az $ 1 9$ területegységnyi négyzet által tartalmazott három pont adta háromszög területe pedig, mint láttuk, legfeljebb $ 1 2\cdot 1 9=1 \right. \kern-\nulldelimiterspace} {18}$ területegység.