Legyen a $ H $ alaphalmaz az egyváltozós valós függvények halmaza, $ M $, $ K $ és $ A $ pedig a $ H $ alábbi részhalmazai:
M = {az értelmezési tartományukon szigorúan monoton növekedő függvények};
K = {az értelmezési tartományukon konvex függvények};
A = {alulról korlátos függvények}.

a) Helyezze el az alábbi hozzárendelésekkel megadott függvények betűjelét az ábra megfelelő részébe!

$ f:\mathbb{R} \rightarrow \mathbb{R},\ x\mapsto \sin x $

$ g:\mathbb{R}\setminus\{0\} \rightarrow \mathbb{R},\ x\mapsto \dfrac{1}{x} $

$ h:\mathbb{R} \rightarrow \mathbb{R},\ x\mapsto 2^x $

$ i:\mathbb{R}^+ \cup \{0\} \rightarrow \mathbb{R},\ x\mapsto \sqrt{x} $

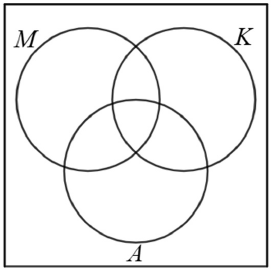
b) Jelölje az ábrán satírozással a $ (K \cap A) \setminus M $ halmazt, és hozzárendelési szabályával adjon meg egy olyan $ j $ függvényt, amely ebbe a halmazba tartozik!
c) Határozza meg az $ \mathbb{R}\rightarrow \mathbb{R}, x\mapsto x^2+bx+c $ függvény $ b $ és $ c $ paramétereinek értékét, ha tudjuk, hogy a függvénynek $ x=2 $-ben minimumhelye van, és a minimum értéke $ –1 $.
d) Határozza meg azokat a $ p \in [0; 2\pi] $ értékeket, amelyekre $ \int\limits_0^p \sin x \,dx=\dfrac{1}{2} $

Megoldás:

a) 

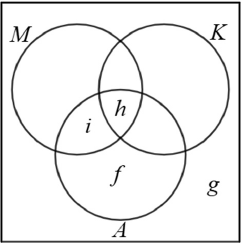
b) 

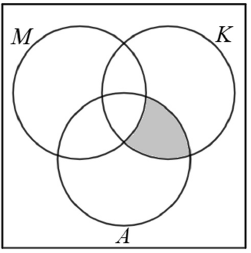
Több függvény is megfelelő (például: $ x^2 $; $ 2^{-x} $)

c) $ b=-4 $; $ c=3 $

d) $ p_1=\dfrac{\pi}{3} $; $ p_2=\dfrac{5\pi}{3} $