Az $ \{a_n\} $ sorozat tagjaira $ n \ge 2 $ esetén az $ a_n=a_{n-1}+n $ összefüggés teljesül. Egy négyszög belső szögei (fokban mérve) $ a_1 $, $ a_2 $, $ a_3 $ és $ a_4 $.
a) Határozza meg a négyszög belső szögeinek nagyságát!
Az $ ABCD $ négyszög oldalai, átlói és szögei közül ismertek a következők: $ AB = 18 $cm, $ AD=15 $cm, $ AC=20 $cm, $ DAB\sphericalangle= 90^\circ $, $ ABC\sphericalangle= 70\sphericalangle $.

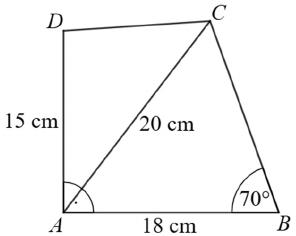
b) Határozza meg a négyszög $ BC $ és $ CD $ oldalának hosszát!

Megoldás:

a) $  86^\circ,\ 88^\circ,\ 91^\circ,\ 95^\circ $

b) $ BC\approx16,83 $cm; $ CD\approx12,27 $cm.