A tengerszint felett h kilométer magasságban mérhető $ p(h) $ légnyomás jól közelíthető a következő képlettel: $ p(h) = p(0) \cdot 10^{0,054\cdot h} $. A képletben $ p(0) $ jelöli a tengerszinten mérhető légnyomást, ami $ 101\,325 Pa $. (A Pa – azaz pascal – a légnyomás mértékegysége.)
a) A Föld legmagasabb hegycsúcsa, a Mount Everest 8848 méter magas. Számítsa ki a megadott képlettel, hogy mekkora a Mount Everest csúcsán mérhető légnyomás!
b) A képlet alapján hány méter magasságban lesz a légnyomás 60 000 Pa? Válaszát 100 méterre kerekítve adja meg!
A Mount Everest meghódítását évtizedek óta kiemelt figyelemmel kíséri a közvélemény. Az alábbi táblázat azoknak a hegymászóknak a számát mutatja (születési hely alapján), akik 2024. szeptemberig legalább kétszer sikeresen feljutottak a csúcsra.2

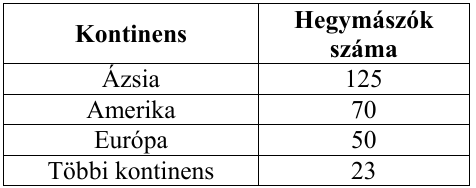
c) Ábrázolja kördiagramon a táblázatban szereplő hegymászók számának kontinensek szerinti megoszlását!
Egy ötfős hegymászócsapat indul a csúcs felé. A csapat tagjai között van Ágnes és László.
d) Hányféle sorrendben haladhatnak öten egymás után, ha Ágnes és László (valamilyen sorrendben) közvetlenül egymás után haladnak?

Megoldás: 

a) $ \approx 33\,723\,Pa $

b) $ \approx 4200 $ méter

c) Jó kördiagram

d) Lehetőségek száma: $2\cdot 4!=48 $