Több mint 60 éves Magyarország egyik kedvelt desszertje, a csokoládéval bevont túrórúd. Az egyik automatába 300 Ft-ot kell bedobni, ha egy ilyen terméket vásárolunk. A gép csak 100 Ft-os és 50 Ft-os érméket fogad el.
a) Hányféleképpen lehet ilyen érmékből 300 Ft-ot bedobni az automatába, ha a bedobás sorrendje is számít? (Az azonos címletű érméket nem különböztetjük meg
egymástól.)
Anna 2 darab tejcsokoládé és 4 darab étcsokoládé bevonatú desszertet vásárolt. A hat desszert közül Balázs véletlenszerűen kiválaszt hármat (visszatevés nélkül).
b) Mennyi a valószínűsége annak, hogy egy darab tejcsokoládé és két darab étcsokoládé bevonatú desszertet választ ki Balázs?
A desszert készítésekor egy 18 mm átmérőjű, 100 mm hosszúságú lehűtött túróhenger köré csokoládébevonatot dermesztenek. A kész desszert alakja egy $ 20 mm \times 10 mm \times 102 mm $ méretű téglatest és egy 20 mm átmérőjű, 102 mm hosszúságú félhenger egyesítésének tekinthető. (A jobb oldali ábrán a desszert keresztmetszeti rajza látható.)

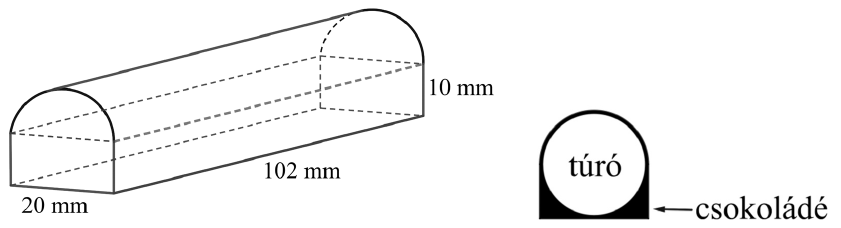
c) Hány $ cm^3 $ csokoládé kerül egy desszertbe?

Megoldás: 

a) 13

b) $ P=\dfrac{6}{10} $

c) $ \approx 10\,975\,mm^3 $, azaz $ \approx 11\,cm^3 $