Az $ ABCD $ négyszögben $ AB=12\, cm $, $ BC=15\, cm $, $ BD=20\, cm $. Az $ A $ csúcsnál lévő belső szög derékszög, továbbá $ DBC\sphericalangle=63^\circ $ (az ábrának megfelelően).

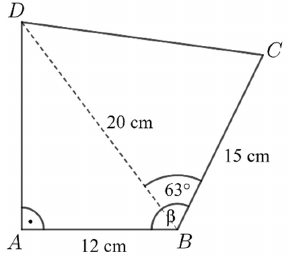
a) Számítsa ki a négyszög $ B $ csúcsnál lévő belső szögének ($ \beta $) nagyságát!
b) Számítsa ki a négyszög $ AD $ és $ CD $ oldalának hosszát, valamint a négyszög területét!
c) Határozza meg az alábbi állítás logikai értékét (igaz vagy hamis)! Válaszát indokolja!

Ha egy négyszög átlói felezik egymást, akkor a négyszög rombusz.

Megoldás: 

a) $ \beta\approx 116,1^\circ $

b) $ AD=16 $ cm; $ CD\approx18,8 $ cm; $ t\approx 230\,cm^2 $

c) Hamis az állítás