Alízék osztálytermében az egyik fal mellett három sorban 12-12, összesen 36 szekrény található a diákok számára, 1-től 36-ig megszámozva. Az osztályba 33-an járnak. Tanév elején minden diák – sorsolás útján – egy-egy szekrényt kap. Három szekrény így a sorsolás után üresen marad.

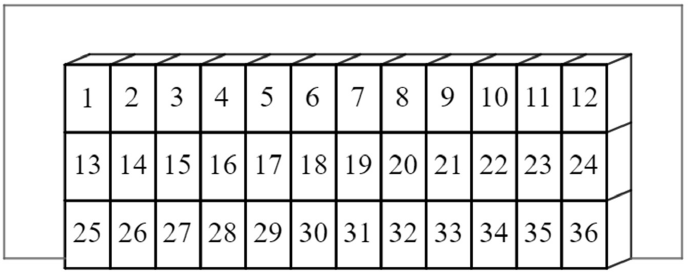a) Legyen az A esemény az, hogy a három üresen maradó szekrény egy sorban található, a B esemény pedig az, hogy a három üresen maradó szekrény három különböző sorban található. Melyik eseménynek nagyobb a valószínűsége?
A szekrények téglatest alakúak. Egy-egy szekrény belseje 20 cm széles, 35 cm magas és 30 cm mély.
b) Határozza meg a leghosszabb egyenes pálca hosszát, ami elhelyezhető a szekrényben! (A pálca vastagságától eltekinthetünk.)
Alíz, Boglárka, Csenge és Dorka szekrénykulcsai összekeveredtek, és a négy lány véletlenszerűen osztja el egymás közt a négy kulcsot.
c) Határozza meg annak a valószínűségét, hogy legalább két lány a saját kulcsát kapja vissza!

Megoldás:

a) $ P_B > P_A $

b) $ \approx 50\ cm $

c) $ P=\dfrac{7}{24}\approx 0,292 $