Egy szabályos dobókockával hatszor dobtunk. A dobott számok monoton növekvő sorrendben: 1, 2, 2, 3, 3, 3.
a) Határozza meg a dobott számok átlagát és szórását!
b) Hány olyan különböző dobássorozat van, amely egy darab 1-esből, két darab 2-esből és három darab 3-asból áll?
Egy szabályos dobókockával kétszer dobunk.
c) Határozza meg annak a valószínűségét, hogy a két dobott szám szorzata 2-vel osztható lesz, de 4-gyel nem!

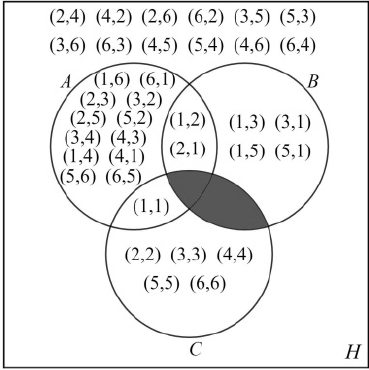
Egy kék és egy zöld dobókockával dobunk, a dobás kimenetele egy számpár. Jelölje (k, z) a dobásnak azt a kimenetelét, amikor a kék kockával dobott szám k, a zöld kockával dobott szám pedig z. Legyen a H alaphalmaz a dobás kimeneteleként megkapható összes lehetséges (k, z) számpár halmaza. Az $ A $, $ B $ és $ C $ részhalmazokat a következőképpen definiáljuk:
$ A $ = {(k, z)│a k + z összeg prím}
$ B $ = {(k, z)│a k $ \cdot $  z szorzat prím}
$ C $ = {(k, z)│k = z}

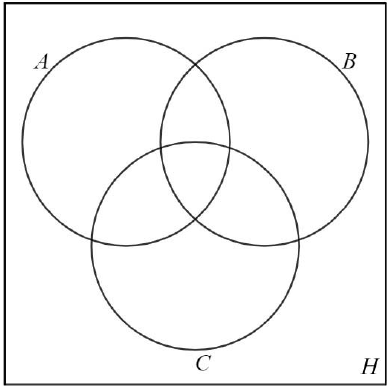
d) Satírozással jelölje a Venn-diagramon a H-nak azt a részhalmazát, amelyik üres halmaz! A Venn-diagram minden egyes további tartományába írjon egy-egy megfelelő számpárt! Válaszát itt nem kell indokolnia.

Megoldás:

a) $ \dfrac{7}{3}\approx 2,33 $

b) $ 60 $

c) $ P=\drfac{1}{3}\approx ,0333 $

d)