Az $ ABCD $ paralelogramma $ AB $ oldala $ 6\,$cm, $ AD $ oldala $ 5\,$cm hosszú, a két oldal által bezárt szög $ 70^\circ$-os.

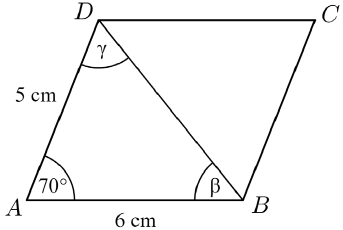a) Számítsa ki az $ ABCD $ paralelogramma területét!
b) Számítsa ki a $ BD $ átló hosszát, valamint az ábrán jelölt $ \beta $ és $ \gamma $ szögek nagyságát!
Tekintsük a következő állítást:
"Ha egy négyszög tengelyesen szimmetrikus, akkor az a négyszög középpontosan is szimmetrikus."
c) Döntse el, hogy az állítás igaz vagy hamis! Válaszát indokolja!
d) Fogalmazza meg az állítás megfordítását, és döntse el a megfordított állításról, hogy igaz vagy hamis! Válaszát indokolja!

 Megoldás:

a) $ T_{ABCD}\approx28,2\,cm^2 $

b) $ BD\approx6,36\,$cm és $ \beta\approx47,6^\circ $ valamint $ \gamma\aaprox 62,4^\circ $

c) Hamis az állítás

d) Megfordítás: Ha egy négyszög középpontosan szimmetrikus, akkor tengelyesen is szimmetrikus.

Hamis az állítás