Egy számítógépes játékban egy kör alakú tartomány az ábra szerint három résztartományra van felosztva (A, B, C). Bármely két tartomány között egy átjáró van (az ábrán szaggatott vonallal jelölve). A tartományok közötti átjárók mindegyike a többitől függetlenül p valószínűséggel van nyitva (0 < p < 1). Egyik tartományból a másikba csak nyitott átjárón (vagy átjárókon) keresztül lehet eljutni.

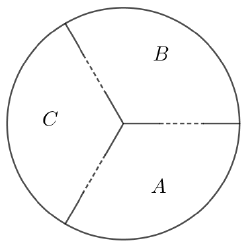
Legyen az $ E_0 $ esemény az, hogy az A tartományból nem lehet másik tartományba eljutni.
a) Mutassa meg, hogy az $ E_0 $ esemény valószínűsége $ 1-2 p+p^2 $ .
b) Hogyan kell megválasztani a $ p $ értékét úgy, hogy az $ E_0 $ esemény valószínűsége legfeljebb 0,01 legyen?
Legyen az E1 esemény az, hogy az A tartományból pontosan egy másik tartományba lehet eljutni, az E2 esemény pedig az, hogy az A tartományból mindkét másik tartományba el lehet jutni (nem feltétlenül közvetlenül).
c) Igazolja, hogy az $ E_1 $ esemény valószínűsége $ 2 p-4 p^2+2 p^3 $ , az $ E_2 $ esemény valószínűsége pedig $ 3 p^2-2 p^3 $ .
d) Határozza meg a $ p $ valószínűség értékét úgy, hogy az $ E_1 $ esemény valószínűsége a lehető legnagyobb legyen, majd számítsa ki ekkor az $ E_1 $

esemény valószínűségét!

Megoldás:

a) Igaz az állítás

b) $ 0,9\le p <1 $

c) Igaz az állítás

d) $ p=\dfrac{1}{3} $