Egy bizonyos fenyőfa (méterben mért) várható magasságának becslésére az alábbi képletet használják:

$ h(t)=\dfrac{30}{1+59\cdot 0,905^t } $

ahol $ t $ a megfigyelés kezdetétől eltelt idő években számítva.
a) Hány méter magas volt a fa a megfigyelés kezdetekor?
b) A megfigyelés kezdetétől számítva hány év múlva lesz a fa 10 méter magas?
c) Számítsa ki az $ \{a_n\} $ sorozat határértékét, ha $ a_n =\dfrac{30}{1+59\cdot 0,905^n} $

Különleges facsemeték neveléséhez egy téglalap alakú részt akarnak elkeríteni.

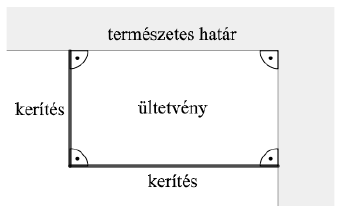
A téglalap két szomszédos oldala természetes határokkal védhető, ezért csak a másik két oldalon kell kerítést építeni. A környezeti adottságok miatt a kerítés építési költsége a két oldalon különböző: az egyik oldalon 5 ezer Ft/m, a másik oldalon pedig 10 ezer Ft/m. A kerítés építésére összesen 400 ezer Ft áll rendelkezésre.

d) Hogyan kell megválasztani a két kerítésszakasz hosszát, hogy a rendelkezésre álló összegből a legnagyobb területű ültetvényt lehessen elkeríteni?

Megoldás:

a) $ 0,5\,m $

b) $ \approx 33,9 $

c) $ 30 $

d) 40 m és 20 m