Egy $(n \times n)$-es táblázat minden mezőjében egy betű áll. A táblázat bármely két sora különböző. Bizonyítsuk be, hogy a táblázatnak van olyan oszlopa, amelyiket elhagyva a megmaradó táblázatnak nincs két egyező sora.

Indirekt úton bizonyítjuk az állítást. Ha a feladat állítása nem volna igaz, akkor minden oszlophoz tartoznék legalább két olyan sor, amelyik csak a kérdéses oszlopbeli betűben különbözik. Minden oszlophoz válasszunk ki egy ilyen sorpárt. Ezt a kiválasztást a következő gráffal (lásd a II. rész 49-52. old. jegyzetét) szemléltethetjük: az $i$-edik sort egy $S_{i}$ ponttal ábrázoljuk, és ha az $i$-edik és $j$-edik sor kiválasztott sorpár, akkor az $S_{i}$ és $S_{j}$ pontot összekötjük egy éllel (1. ábra). Gráfunknak n pontja van és ugyanannyi éle. Egy ilyen gráfban mindig van kör, vagyis olyan különböző pontokból álló $S_{i_1 } ,S_{i_2 } ,...,S_{i_k } $sorozat, amelyben $S_{i_j } $-t $S_{i_{j+1} } $-gyel \textit{(i = 1,{\ldots}, k - }1 ) és $S_{i_k } $-t $S_{i_1 } $-gyel él köti össze. Ha ugyanis egy $n$-pontú gráfban nincs kör, akkor annak legfeljebb $n -$ 1 éle lehet. Ezt a megoldás végén bizonyítjuk. A fenti kör a táblázatra vonatkozóan azt jelenti, hogy az $i_{l}$-edik és $i_{2}$-edik sor csak egy betűben, mondjuk a $j-$edik oszlopbeliben különbözik, az előbbiben itt egy $a_{l}$, az utóbbiban egy ettől különböző $a_{2}$ betű áll. Az $i_{2}$-edik és $i_{3}$-adik sor is csak egy betűben különbözik, és ezek egy másik oszlopban állnak, tehát az $i_{3}$-adik sor $j$-edik betűjele szintén $a_{2}$. Hasonlóan az $i_{4}$-edik, {\ldots}, $i_{k}$-adik sor $j$-edik betűje is $a_{2}$, de az $i_{k}$-adik és $i_{1}$-edik sor is csak egy betűben tér el, és ezek is egy, a $j$-ediktől különböző oszlopban állnak. Így az $i_{1}$-ellik sor $j$-edik betűje is $a_{2}$ kellene, hogy legyen, holott ott az $a_{2}$-től különböző $a_{1}$ betű áll. Abból a feltevésből tehát, hogy bármelyik oszlop elhagyásával keletkezik két egyező sor, ellentmondásra jutottunk. Így kell olyan oszlopnak lennie, amelyet elhagyva továbbra is minden sor különböző lesz.

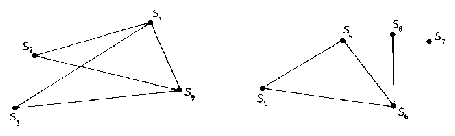
A felhasznált segédtétel bizonyítása: Egy $n$-pontú gráf egy vagy több összefüggő részből áll, vagyis olyanból, amelyiknek bármelyik pontjából el lehet jutni élek mentén haladva az összes többibe * (1. ábra). (* Egy-egy ilyen rész állhat egyetlen pontból is.) A következő segédtételt bizonyítjuk: Ha egy összefüggő gráfnak k pontja van és nincs benne kör, akkor k - 1 éle van. A szögpontok számára vonatkozó teljes indukcióval bizonyítunk. Ha a gráfnak 1 vagy 2 szögpontja van, akkor az 1 pont, illetve a két pontot összekötő él, tehát az élek száma 0, illetve 1 a tételnek megfelelően. Ha a tétel igaz $n $szögpontú gráfokra, és adva van egy $n + $ 1 szögpontú $G$ gráf, amelyik kielégíti a tétel feltételeit, akkor válasszunk ki egy PP' élt, hagyjuk el, és a két végpontját vonjuk össze egy $P*$ szögponttá (2. ábra). Az új $G'$ gráf $P*$ pontja $G$ -ben $P$-nek és $P'$-nek felel meg, a többi szögpontja $G$ egy-egy szögpontjának, minden éle egy-egy élének felel meg kölcsönösen egyértelműen. Belátjuk, hogy $G'$ is kielégíti a tétel feltételeit. Két pontjához tekintsük $G$ megfelelő szögpontjait, ha az egyikük $P*$, akkor pl. $P$-t és az ezeket összekötő utat. Ennek megfelel $G -$ben egy (esetleg egy éllel rövidebb) összekötő út. Ha $G'$-ben volna kör, akkor annak át kellene mennie $P*$-on, mert különben kör felelne meg neki $G$ -ben is. Ez volna a helyzet akkor is, ha a kör mindkét $P*$ végpontú élének $P$ végpontú vagy mindkettőnek $P'$ végpontú felelne meg $G$-ben. Ha viszont a $G'$-beli kör egyik $P*$ végpontú élének $P$ végpontú él felelne meg, a másiknak $P'$ végpontú, akkor a PP' éllel együtt kapnánk $G$-beli kört. Nem lehet tehát $G'$-ben $P*$-on átmenő kör sem.

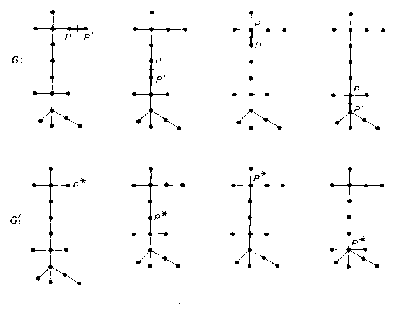
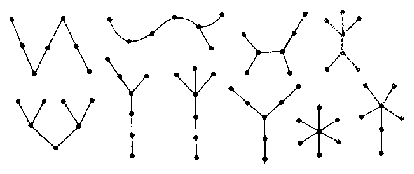
Az indukciós feltevés szerint így $G'$-nek $n - $ 1 éle van, tehát $G$ -nek $n $éle. Ezzel beláttuk a tétel érvényességének öröklődését is. A tétel tehát igaz minden $k$-ra. Jegyzet. Fa alakú gráfok, élszámuk. Az összefüggő, kört nem tartalmazó gráfokat fa alakú gráfnak, vagy röviden fának nevezik. Ilyennel találkoztunk, ha nem is megnevezve az 1970/3. feladatban (90. old.). Az ott szereplő alakzat lényegében egy véges teljes gráf. (A szereplő fogalmakra vonatkozóan lásd a II. rész 58-59. old. jegyzetét.) Abban a kiszínezett szakaszok egy fa alakú részgráfot alkotnak, amelyik kifeszíti a gráfot. A szögpontok száma, ha nagyobb 3-nál, még távolról sem határoz meg egy fát (3. ábra). A bizonyított segédtétel szerint az élek számát azonban már meghatározza. Egy k szögpontú, fa alakú gráfnak k - 1 éle van.

2. Megoldás

A következő, a feladatbelinél valamivel általánosabb állítást bizonyítjuk be teljes indukcióval. Ha egy táblázatnak legalább annyi oszlopa van, mint sora, és a táblázat mindegyik mezejére egy betűt írunk úgy, hogy bármely két sor különbözzék, akkor van olyan oszlop, amelyiknek az elhagyása után is különböző sorok különböző módon lesznek kitöltve . Két sor esetén van legalább két oszlop és van közöttük olyan, amelyikben a két sorban különböző betűk állnak. Bármelyik további oszlopot (ha több van, akár mindet együtt is) elhagyhatjuk. Tegyük most fel, hogy $n$-nél kevesebb soros (és legalább ugyanannyi oszlopos) táblázatra igaz az állítás, és vegyünk egy $n $soros táblázatot, amelyik kielégíti az állítás feltételeit. Hagyjuk el az első oszlopot. Ha a sorok ezután is páronként különbözők, akkor az állítás igaz. Ha bizonyos sorok így egyenlővé váltak, akkor az egyenlővé vált sorok közül csak egyet-egyet tartsunk meg. Így eggyel fogyott az oszlopok száma és legalább egy sort is elhagytunk, tehát továbbra is legalább annyi oszlop van, mint sor, továbbá bármely két sor különböző. Erre a táblázatra feltevés szerint igaz az állítás: elhagyható egy oszlop úgy, hogy a sorok mind különbözők maradjanak. Hagyjuk el a megfelelő oszlopot az eredeti táblázatból és nézzünk két sort. Ha mindkettő szerepelt a megritkított táblázatban is, akkor különbözők már akkor is, ha az első betűket figyelmen kívül hagyjuk. Ha viszont egy olyan csoportban vannak, amiből csak egy sor került a megritkított táblázatba, akkor az első betűk különbözők. Ekkor is találtunk tehát olyan oszlopot, amelyiknek az elhagyása után bármely két sor különböző maradt. A tulajdonság tehát öröklődik az $n$-soros táblázatokra is.
Megjegyzések. 1. A II. megoldásban bizonyított állítás helyessége is bizonyítható az I. megoldás módszerével. Mindössze annyi változik, ha $n$-nél több oszlop van az $n$-soros táblázatban, hogy a megoldásban szereplő gráfnak $n$-nél több éle lesz. 2. Ha csak eggyel is kevesebb oszlop van, mint amennyi sor, akkor már nem bizonyos, hogy van elhagyható oszlop. Ez leolvasható a 4. ábra táblázatáról.

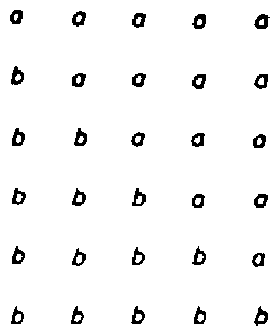
3. A feladat állításának helyességére az ábécé betűinek a számából próbálni következtetni zsákutca, hiszen már két betűvel is ki lehet tölteni a táblázatot a feltételeknek megfelelően. Egy ilyen kitöltést kapunk, ha az előző megjegyzés táblázatát egy csupa $a$-ból álló oszloppal egészítjük ki.