(Feladat azonosítója: AD_20222023_h3k1f4f )
Témakör: *Kombinatorika
Egy szabályos háromszög minden oldalát n egyenlő részre osztjuk, majd az osztáspontokon át a megfelelő oldalakkal párhuzamosakat húzva felosztjuk a háromszögünket n2 darab kisebb szabályos háromszögre. Ezek után a kisebb háromszögek közül néhánynak megrajzoljuk az egyik súlyvonalát arra figyelve, hogy egyetlen súlyvonalnak se legyen semelyik másik súlyvonallal közös (vég)pontja. Például az alábbi ábrán n = 3 esetén mind a kilenc kisebb háromszög egy-egy súlyvonalát megrajzoltuk. Jelölje $ s(n) $ azt a legnagyobb számot, amennyi súlyvonal szabályosan berajzolható adott n esetén. (A lenti ábra alapján $ s(3) = 9 $ például.)
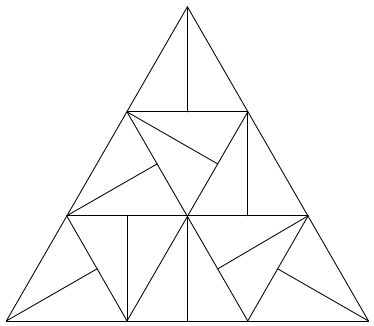
Megoldás:
$ s(n)=min \left( n^2; \dfrac{(n+1)(n+2)}{2} \right) $