Egy felül nyitott doboz vízszintes asztallapon áll. A dobozt három téglalap és két derékszögű trapéz határolja. A doboznak a vízszintes síkra illeszkedő lapja 8 cm × 6 cm méretű, két egymással szemközti függőleges síkú lapja pedig 6 cm × 5 cm, illetve 6 cm × 2 cm méretű téglalap.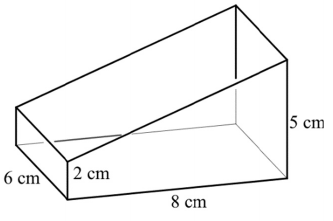
a) Számítsa ki a doboz testátlóinak hosszát!
A test kiterített hálóját az ábra sötétített tartománya szemlélteti. Ezt a hálót egy 15 cm × 16 cm-es téglalapból vágjuk ki (ennek oldalai párhuzamosak a test 8 cm × 6 cm-es alaplapjának oldalaival).

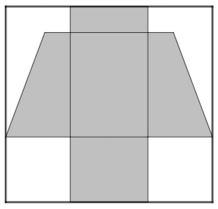
b) Hány százalék hulladék keletkezik?
Egy téglalap alakú kartonlap oldalhosszait úgy szeretnénk megválasztani, hogy alul és felül 4-4 cm-es, jobb és bal oldalon 2-2 cm-es margót hagyva a lap közepén megmaradó téglalap alakú terület 50 cm 2 nagyságú legyen.

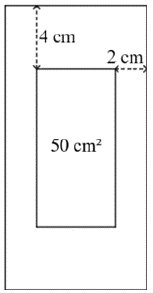
c) Mekkorának válasszuk a kartonlap oldalainak hosszát, hogy a területe a lehető legkisebb legyen?

Megoldás:

a) $ \sqrt{125}\approx 11,2\,$cm

b) $ 39,2\% $

c) 9 cm és 18 cm