Két forgáshenger alakú viaszgyertyánk van. Az egyik gyertya alapkörének sugara $ r $, magassága $ h $, a másik alapkörének sugara $ R $, magassága szintén $ h $. A két gyertyát összeolvasztjuk, majd a viaszból egy ugyancsak $ h $ magasságú, forgáshenger alakú gyertyát öntünk ($ r, h, R > 0 $).
a) Igazolja, hogy az így kapott gyertya alapkörének sugara legalább $ \sqrt{2rR} $. (Az öntés során fellépő anyagveszteségtől eltekinthetünk.)
Egy forgáshenger alakú tortát egy 15 cm sugarú, félgömb alakú védőbúra alatt helyezünk el. A torta a félgömb határoló körének síkján áll, és a torta fedőlapjának határoló köre a félgömbre illeszkedik (az ábra szerint).

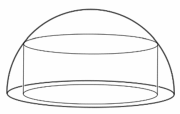
b) Igazolja, hogy az $ m $ cm magasságú torta térfogata (köbcentiméterben mérve) $ 225 π m − π m^3 $. ($ 0 < m < 15 $)
c) Igazolja, hogy a védőbúra alatt (a fent leírt módon) elhelyezhető maximális térfogatú torta térfogata kisebb, mint a félgömb térfogatának 60\%-a!

Megoldás:

a) Igaz az állítás

b) Igaz az állítás

c) Igaz az állítás