(Feladat azonosítója: mme_202110_2r08f )
Témakör: *Geometria
Egy áruházláncban minden Kocka csokoládé vásárlásakor a csoki mellé ajándékba adnak egy „zsákbamacska” csomagot, amelyben egy kis fémkocka van. A fémkocka mindegyik lapja sárga vagy kék színűre van festve úgy, hogy mind a két színű lap előfordul.
a) Igazolja, hogy (színezés szerint) összesen 8-féle kocka van, ha a forgatással egymásba vihető színezéseket nem tekintjük különbözőnek!
b) Dórinak 7 különböző színezésű kockája van, így már csak egy hiányzik a teljes készlethez, hogy abból nyakláncot készítsen magának. Mennyi annak a valószínűsége, hogy ha 3 darab Kocka csokoládét vesz, akkor meglesz a teljes készlete? (Feltételezhetjük, hogy mindegyik kockafajta ugyanakkora valószínűséggel fordul elő a csomagokban.)
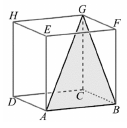
Az ábrán látható $ ABCDEFGH $ kocka élhosszúsága 10 egység.
c) Számítsa ki az $ ABG $ háromszög beírt körének sugarát!
Megoldás:
a) Igaz az állítás
b) $ P=1-\left( \dfrac{7}{8} \right)^3\approx 0,330 $ az egyenes egyenlete
c) $ r=\dfrac{50\sqrt{2}}{5+5\sqrt{2}+5\sqrt{3}}\approx 3,41 $