(Feladat azonosítója: mme_202005_2r05f )
Témakör: *Algebra
Az északi félteke 50. szélességi körén egy adott napon a nappal hosszát (a napkelte és a napnyugta között eltelt időt) jó közelítéssel a következő f függvénnyel lehet modellezni:
$ f(n)= -5,2\cos\left( \right)\dfrac{n+8}{58 }+11,2 $
ahol $ n $ az adott nap sorszámát jelöli egy adott éven belül, $ f(n) $ pedig a nappal hossza órában számolva $ (1 \le n \le 365 $, $ n \in \mathbb{N} )$.
Az alábbi ábra a $ g : [ 1;365 ] \rightarrow \mathbb{R}$; $g ( x) = -5,2\cos\left( \right)\dfrac{n+8}{58 }+11,2 $függvényt szemlélteti. (A $ g $ függvény az $ f $-nek egy folytonos kiterjesztése.)
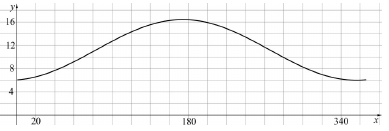
a) Ha $ x = 1 $, akkor $ \dfrac{x+8}{58} $ helyettesítési értéke $ \dfrac{9}{58} $. Adja meg a $ \dfrac{9}{58} $ radián értékét fokban mérve!
b) Számítsa ki a modell alapján, hogy az év 50. napján milyen hosszú a nappal! Válaszát óra:perc formátumban, egész percre kerekítve adja meg!
c) Igazolja, hogy (a modell szerint) egy évben 164 olyan nappal van, amelyik 12 óránál hosszabb!
Adott egy másik, az $ y = -5,2 \cos(x) + 11,2 $ egyenletű görbe, valamint az $ x = 0 $, az $ y = 0 $ és az $ x = 2\pi $ egyenletű egyenesek.
d) Számítsa ki a görbe és a három egyenes által határolt korlátos síkidom területét!
Megoldás:
a) $ \approx 8,89^\circ $
b) 8 óra 23 perc
c) Igaz az állítás
d) $ \approx 70,37 $