A mellékelt ábrán egy kereszt alakú lemez látható, amely 5 db 10 cm oldalú négyzetből áll. A lemezből egy 10 cm alapélű, szabályos négyoldalú gúla hálóját szeretnénk kivágni úgy, hogy a középső négyzet legyen a gúla alaplapja.

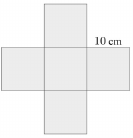
a) Igazolja, hogy a lehetséges hálók kivágása során keletkező hulladék legalább $ 200 cm^2 $, de kevesebb $ 300 cm^2 $-nél! 

Tekintsük az ábrán látható nyolcpontú gráfot.

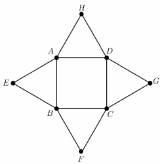
b) A gráfban véletlenszerűen kiválasztunk két csúcsot. Mennyi a valószínűsége annak, hogy a két csúcsot él köti össze a gráfban?
c) A gráf 9 élét kékre, 3 élét pedig zöldre színezzük. Igazolja, hogy bármelyik ilyen színezésnél lesz a  gráfban egyszínű (gráfelméleti) kör!

Megoldás:

a) Igaz az állítás

b) $ P=\dfrac 3 7 $

c) Igaz az állítás