(Feladat azonosítója: mmk_202005_2r18f )
Témakör: *Geometria
Egy sétálóutca díszburkolatát ötszög alapú egyenes hasáb alakú kövekkel készítik el. (Az ábrán négy ilyen követ lehet látni a burkolaton megfigyelhető elrendezésben.)
 A kő alapját képező $ ABCDE $ ötszög tengelyesen szimmetrikus (egy, a $ D $ csúcson átmenő egyenesre), négy oldala $ 10 cm $ hosszú, három szöge $ 120\sphericalangle $-os, az ábrának megfelelően.
A kő alapját képező $ ABCDE $ ötszög tengelyesen szimmetrikus (egy, a $ D $ csúcson átmenő egyenesre), négy oldala $ 10 cm $ hosszú, három szöge $ 120\sphericalangle $-os, az ábrának megfelelően.
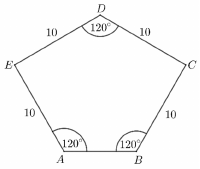
a) Számítással igazolja, hogy az $ AED $ és a $ BCD $ háromszög derékszögű!
b) Számítsa ki az $ ABCDE $ ötszög területét!
Róbert egy járdaszakaszt egyedül 20 óra alatt burkolna le ezzel a kővel, Sándor ugyanazt a munkát egyedül 30 óra alatt végezné el.
c) Mennyi idő alatt végeznek, ha együtt dolgoznak?
Ezt a követ szürke és sárga színben árulják a kereskedésben. A dobozokon matrica jelzi a dobozban lévő kövek színét. Átlagosan minden századik dobozon rossz a matrica: szürke helyett sárga vagy fordítva. (Ezt tekinthetjük úgy, hogy 0,01 annak a valószínűsége, hogy rossz matrica került a dobozra.) Péter kiválaszt 21 szürke jelzésű dobozt, és ellenőrzi a dobozokban lévő kövek színét.
d) Mennyi a valószínűsége annak, hogy a 21 kiválasztott doboz közül legalább 20 dobozban valóban szürke kő van?
Megoldás:
a) Igaz az állítás
b) $ 150 cm^2 $
c) 12 óra
d) $ \approx 0,9815 $