Egy kétszemélyes társasjátékot olyan négyzet alakú táblán játszanak, amelyet fehér és szürke mezőkre osztottak fel az ábra szerint.

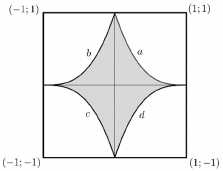
Ha a táblát egy olyan koordináta-rendszerbe helyezzük, amelyben a négyzet csúcsainak koordinátái $(1; 1)$, $(–1; 1)$, $(–1; –1)$, illetve $(1; –1)$, akkor ebben a koordináta-rendszerben az a jelű ív egyenlete: $y = (1 - x )^3$, $ 0 \le x \le 1$. A tábla középpontosan és tengelyesen is szimmetrikus.

a) Írja fel a másik három (az ábrán b, c, illetve d jelű) ív egyenletét is!

A társasjáték gyártója a 2 dm oldalú tábla fehér színű részének bevonásához egy speciális anyagot használ. Ebből 1 kg mennyiség 12 $m^2$ terület bevonásához elegendő.

b) Számítsa ki, hogy 4000 darab tábla elkészítéséhez hány kg speciális anyag szükséges!

A kétszemélyes társasjátékban minden játszma csak valamelyik játékos győzelmével végződhet, döntetlen nincs. Minden játszmában 1 pontot kap a győztes, a vesztes pedig 0 pontot. Anna és Bori nagyon szereti ezt a társasjátékot, sok játszmát lejátszottak már. Ha egymás ellen játszanak, akkor Anna 0,4 valószínűséggel, Bori pedig 0,6 valószínűséggel nyer meg egy játszmát. Egyik alkalommal megállapodnak, hogy addig játszanak újabb játszmákat, amíg valamelyikük először éri el a 10 pontot (és így megnyeri a játékot).

c) Mennyi annak a valószínűsége, hogy Bori legfeljebb 12 játszma után megnyeri a játékot? (Kezdéskor mindkettőjüknek 0 pontja van.)

Megoldás:

a) b ív: $y=(x+1)^3;\qquad -1 \le x \le 0$

c ív: $y=-(x+1)^3;\qquad -1 \le x \le 0$

d ív: $y=(x-1)^3;\qquad 0 \le x \le 1$

b) 10 kg

c) $P\approx 0,083$