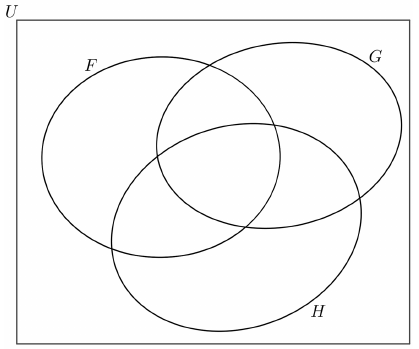
Legyen az $U$ alaphalmaz a legalább 4 pontú egyszerű gráfok halmaza. Az $F$ halmaz az $U$ elemei közül pontosan azokat tartalmazza, amelyek fagráfok, a $G$ halmaz pontosan azokat, amelyek összefüggő gráfok, a $H$ halmaz pedig pontosan azokat, amelyek 6 pontú gráfok.

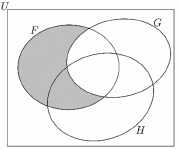
a) Az alábbi ábrán satírozással jelölje meg, és halmazműveletekkel is adja meg az $U$-nak azt a részhalmazát, amelyik üres halmaz!

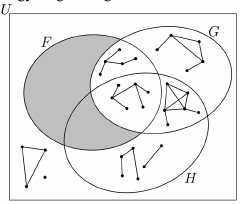
b) A megadott Venn-diagram minden egyes további részébe rajzoljon pontosan egy lehetséges gráfot!

Egy telephely $K$, $L$, $M$, $N$, $O$, $P$, $Q épületei közül az éjszakai első ellenőrzés során ötöt ellenőriz a biztonsági őr.

c) Hányféleképpen tervezheti meg az útvonalát, ha a $K$ és $L$ épületeket mindenképpen ellenőrzi? (Két útvonal különböző, ha a két út során más épületeket, vagy ugyanazokat az épületeket, de más sorrendben ellenőriz a biztonsági őr.)

Megrajzoltuk az $ABCDE$ konvex ötszög oldalait és átlóit, majd a megrajzolt szakaszok mindegyikét vagy kékre, vagy zöldre színeztük. A színezés befejezése után észrevettük, hogy nincs olyan háromszög, amelynek csúcsai az $A$, $B$, $C$, $D$, $E$ pontok közül valók, és mindhárom oldala azonos színű.

d) Igazolja (például indirekt módszerrel), hogy nincs olyan csúcsa az ötszögnek, amelyből legalább három azonos színű szakasz indul ki!

Megoldás:

a)

b) Például:

c) 1200

d) -