Öt különböző számjegyet leírunk egy papírlapra. Két számjegyet pontosan akkor kötünk össze egy vonallal (éllel), ha a különbségük páros szám (de egyik számjegyet sem kötjük össze önmagával). Így egy ötpontú gráfot kapunk.

a) Határozza meg az alábbi két állítás logikai értékét (igaz vagy hamis)! Válaszát indokolja!

I. Lehetséges, hogy fagráfot kapunk.

II. Lehetséges, hogy nem összefüggő gráfot kapunk.

Az Óceán Légitársaságnak a megalakulása óta alapelve, hogy a szigetvilágban működő hálózatának bármely két célállomása között működtet repülőjáratot. (Az ábra azt a több évvel ezelőtti időszakot szemlélteti, amikor még csak négy célállomás és hat repülőjárat volt.)

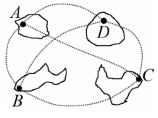
A hálózatot folyamatosan bővítik: az utóbbi két év alatt a célállomások száma másfélszeresére nőtt, ugyanezen idő alatt a repülőjáratok száma pedig 60-nal lett több.

b) Hány célállomásra közlekednek jelenleg?

A légitársaság vezetőségi értekezletén megállapították, hogy az 1-es számú járatukon legfeljebb 168 utasnak van hely, de minden alkalommal sokkal többen szeretnének jegyet váltani. Több év tapasztalatai szerint 0,032 annak a valószínűsége, hogy erre a járatra valaki megveszi a jegyet, de aztán valamilyen ok miatt mégsem jelenik meg a járat indulásánál. Emiatt a vezetőség úgy dönt, hogy erre a 168 fős járatra ezentúl 170 jegyet adnak el. Az érvényes szabályozás szerint a több jegy eladása miatt a járatról esetleg lemaradó utasoknak a légitársaság fejenként 600 euró kártérítést köteles fizetni.

c) Ha a vezetőség megállapításai helyesek, akkor mennyi a valószínűsége annak, hogy az 1-es számú járat egy indulásánál legfeljebb 168 utas jelenik meg, és mennyi a társaság által fizetendő kártérítés várható értéke a járat egy útját tekintve?

Megoldás:

a) I. hamis, II. igaz

b) 15 célállomás

c) P=0,974 ls 18 eiró