(Feladat azonosítója: mmk_201905_2r18f )
Témakör: *Algebra
Az ábrán egy kis múzeum alaprajzát látjuk.
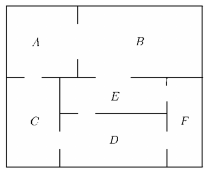
A múzeum termei közötti kapcsolatot gráffal is szemléltethetjük. A gráf pontjai a termek, élei pedig az átjárók a termek kö- zött. (Egy él egy átjárót szemléltet két terem között.)
a) Rajzolja fel a múzeum termeit és átjáróit szemléltető gráfot!
A múzeumba háromféle belépőjegyet lehet váltani:

Januárban négyszer annyi kedvezményes belépőjegyet adtak el, mint teljes árú jegyet, továbbá az eladott fotójegyek száma az eladott teljes árú jegyek számának $ 12,5\% $-a volt. A múzeum belépőjegy-eladásból származó bevétele januárban 912 600 Ft volt.
b) Hány belépőjegyet adtak el januárban összesen?
Csilla, Dezső, Emese, Feri és Gyöngyi délelőtt 10-re beszéltek meg találkozót a múzeum előtt. Sorban egymás után érkeznek (különböző időpontokban), véletlenszerűen.
c) Mennyi a valószínűsége annak, hogy legfeljebb egy lánynak kell várakoznia fiúra?
A kiállításon több gondolkodtató, minimalista kép is szerepel. Dezső szerint az ábrán látható, csatlakozó félköröket ábrázoló kép címe azért "Egyenlőség", mert a felső és az alsó görbe vonal hossza egyenlő.
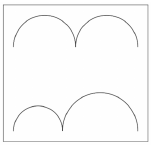
A felső görbét alkotó két egyforma félkör átmérőjének összege 48 cm. Az alsó görbét alkotó két félkör átmérőjének összege szintén 48 cm.
d) Igaz-e Dezső sejtése, hogy a két görbe vonal hossza egyenlő?
Megoldás:
a) Grág rajzolás
b) 3198
c) $ 30\% $
d) Dezsőnek igaza van.