A Föld teljes vízkészlete (jég, víz és vízgőz) folyékony halmazállapotban közel 1400 millió $ km^3 $lenne. Ennek a vízkészletnek csupán $ 3\% $-a édesvíz, melynek valójában mindössze $ 20\% $-a folyékony halmazállapotú (a többi főleg a sarkvidék jégtakarójában található fagyott, szilárd állapotban). a

) Számítsa ki, hogy hány kilométer lenne annak a legkisebb gömbnek a sugara, amelybe összegyűjthetnénk a Föld folyékony édesvízkészletét! Válaszát egész kilométerre kerekítve adja meg!

Az ábrán egy környezetvédő szervezet logójának ki nem színezett terve látható.

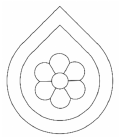
A logó kilenc tartományát három színnel (sárga, kék és zöld) szeretnénk kiszínezni úgy, hogy a szomszédos tartományok kü- lönböző színűek legyenek. (Két tartomány szomszédos, ha a határvo- nalaiknak van közös pontja. Egy-egy tartomány színezéséhez egy színt használhatunk.)

b) Hányféleképpen lehet a logót a feltételeknek megfelelően kiszínezni?

Egy iskolai italautomata meghibásodott, és véletlenszerűen ad szénsavas, illetve szénsav- mentes vizet. A diákok tapasztalata szerint, ha valaki szénsavmentes vizet kér, akkor csak 0,8 a valószínűsége annak, hogy valóban szénsavmentes vizet kap. Anna a hét mind az öt munkanapján egy-egy szénsavmentes vizet szeretne vásárolni az automatából, így minden nap az ennek megfelelő gombot nyomja meg.

c)Mennyi a valószínűsége annak, hogy legalább négy napon valóban szénsavmentes vizet ad az automata?

 Megoldás:

a) 126 lm

b) 12

c) $\approx 73,8\% $