Adott az $ f: R \rightarrow R, f (x) = x^2 + 4x + 3 $ függvény.

a) Írja fel két elsőfokú tényező szorzataként az $ x^2 + 4x + 3 $ kifejezést!

b) A $ P(–6,5; y) $ pont illeszkedik az $ f $ grafikonjára. Számítsa ki $ y $ értékét!

c) Az alábbi grafikonok közül válassza ki az $ f $ függvény grafikonját (karikázza be a megfelelő betűt), és határozza meg az $ f $ értékkészletét!

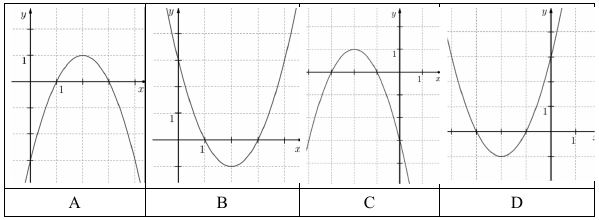
Adott a $ g: R \rightarrow R, g (x) = x^2 - 6 x + 5 $ függvény. Az a három pont, ahol a $ g $ grafikonja
metszi a koordinátatengelyeket, egy háromszöget határoz meg.

d) Határozza meg ennek a háromszögnek a területét!

 Megoldás:

a) $(x+1)(x+3) $

b) $ y=19,25 $

c) D grafikon és $ y \in [1;\infty ) $

d) $ t=10 $