Barnabás telefonján a képernyő átlója $ 5,4\ col $  $ (1\ col \approx 25,4\ mm) $, a képernyő oldalainak aránya $ 16 : 9 $. A telefon téglalap alakú előlapján a képernyő alatt és felett $ 12-12 mm$, két oldalán $ 3-3 mm $ szélességű szegély van.

a) Mekkorák a telefon előlapjának oldalai? Válaszát egész mm-re kerekítve adja meg!

Az írásbeli érettségi vizsga megkezdése előtt a felügyelő tanár megkéri a vizsgázókat, hogy telefonjaikat kikapcsolt állapotban tegyék ki a tanári asztalra. Általános tapasztalat, hogy egy-egy diák a "vizsgaláz" miatt 0,02 valószínűséggel bekapcsolva felejti a telefonját.

b) Mekkora annak a valószínűsége, hogy a teremben lévő 12 vizsgázó közül legalább egy bekapcsolva felejti a telefonját?

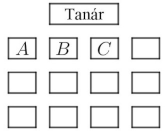
A vizsgateremben lévő 12 egyszemélyes pad négy egymás melletti oszlopba van rendezve. Mindegyik oszlopban három egymás mögötti pad áll. Julcsi és Tercsi jó barátnők, elhatározzák, hogy a vizsgán két egymás melletti padba ülnek. (Például ha Julcsi a B-vel jelölt padban ül, akkor Tercsi az A vagy C jelű padot foglalja el.)

c) Hányféleképpen ülhet le a 12 vizsgázó a teremben úgy, hogy Julcsi és Tercsi valóban két egymás melletti padban üljön?

Az iskolában érettségiző 100 tanuló matematika írásbeli érettségi vizsgájának pontszámairól készült összesítést mutatja a táblázat.

d) A táblázat alapján mennyi a 100 tanuló pontszámának lehetséges legmagasabb átlaga?

Megoldás:

a) a telefon előlapjának oldalai 144 mm és 73 mm hosszúak

b) $ 1- 0,98^{ 12 } \approx 0,215 $

c) 65 318 400

d) 66