Adott egy AB szakasz, s rajta tetszőlegesen 2017 pont. A szakaszra az ábrán látható módon adott α szögű egyenlőszárú háromszögeket rajzolunk.

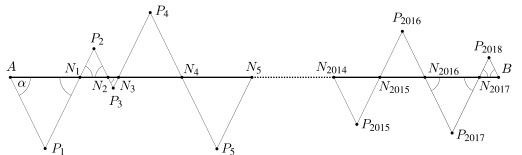
a) Hogyan vegyük fel a pontokat, hogy ezen háromszögek területeinek összege minimális legyen?

b) Hogyan vegyük fel a pontokat, hogy az AP₁N₁P₂N₂ . . . P₂₀₁₈B töröttvonal hossza a legnagyobb legyen?

Megoldás: a) A pontok egyenletesen helyezkednek el. 

b) A töröttvonal hossza állandó a pontok helyének megválasztásától függetlenül.