Bizonyítsuk be, hogy ha egy háromszög $a, b, c$ oldalára teljesül a $ 2\left( {a+b} \right)=3c$ összefüggés, ahol $a\langle b\langle c$, továbbá a $\underline{c}$ oldallal szemközti szög kétszerese az $\underline{a}$ oldallal szemközti szögnek, akkor $\frac{a+c}{2}=b$.

Tekintsük a következő ábrát! Ábránk jelölései alapján az ABC és CBD háromszög hasonló, hiszen szögeik megegyeznek, ezért a megfelelő oldalaik aránya is egyenlő.

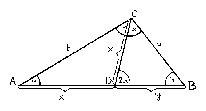
Ezek alapján $\frac{a}{y}=\frac{c}{a}$, azaz $y=\frac{a^2}{c}$. Az ADC háromszög egyenlő szárú $\left( {AD=DC=x} \right)$, így $\frac{b}{x}=\frac{c}{a}$, azaz $x=\frac{ab}{c}$. Mivel $AD+DB=x+y=c$, ezért $\frac{ab}{c}+\frac{a^2}{c}=c$, ahonnan $b=\frac{c^2-a^2}{a}$ adódik. A feladat feltétele alapján $b=\frac{3c-2a}{2}$, így $\frac{c^2-a^2}{a}=\frac{3c-2a}{2}$. Rendezett alakban pedig $ 2c=3a$ adódik. Mindkét oldalhoz $c-2a$ értékét hozzáadva pedig a $ 3c-2a=a+c$ összefüggést kapjuk, ahonnan 2-vel osztva a bizonyítandó $\frac{3c-2a}{2}=b=\frac{a+c}{2}$ állításhoz jutunk.