Az $\overrightarrow{AB}$ és $\overrightarrow{AC}$ vektorok 120°-os szöget zárnak be egymással, és mindkét vektor hossza 5 egység.

a) Számítsa ki az $\overrightarrow{AB}+\overrightarrow{AC}$ vektor hosszát!

b) Számítsa ki az $\overrightarrow{AB}-\overrightarrow{AC}$ vektor hosszát!

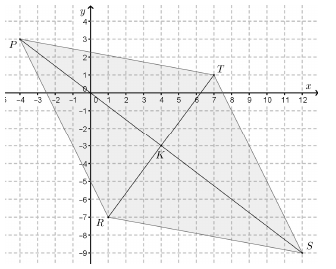
A PRST rombusz középpontja a K (4; –3) pont, egyik csúcspontja a T (7; 1) pont. Tudjuk, hogy az RT átló hossza fele a PS átló hosszának.

c) Adja meg a P, az R és az S csúcsok koordinátáit!

Megoldás: a) 5; b) $ 2\cdot5\cdot\dfrac{\sqrt{3}}{2} \approx 8,66$ c) R (1; –7); P (–4; 3); S (12; –9).