Egy öttusaversenyen 31 résztvevő indult. A vívás az első szám, ahol mindenki mindenkivel egyszer mérkőzik meg. Aki 21 győzelmet arat, az 250 pontot kap. Aki ennél több győzelmet arat, az minden egyes további győzelemért 7 pontot kap a 250 ponton felül. Aki ennél kevesebbszer győz, attól annyiszor vonnak le 7 pontot a 250-ből, ahány győzelem hiányzik a 21-hez. (A mérkőzések nem végződhetnek döntetlenre.)

a) Hány pontot kapott a vívás során Péter, akinek 5 veresége volt?

b) Hány győzelme volt Bencének, aki 215 pontot szerzett?

Az öttusa úszás számában 200 métert kell úszni. Az elért időeredményekért járó pontszámot mutatja a grafikon.

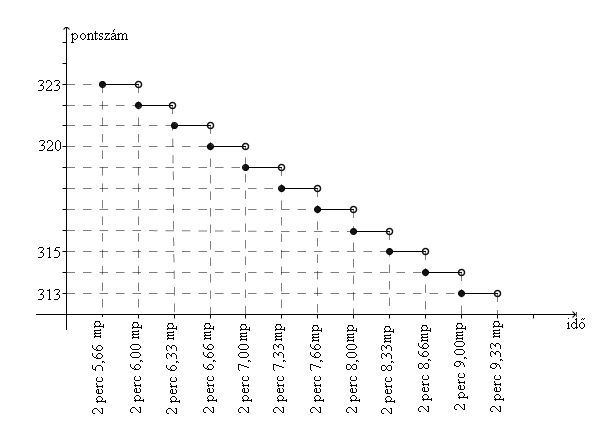
c) Jelölje meg az alábbi két kérdés esetén a helyes választ!

Hány pontot kapott Robi, akinek az időeredménye 2 perc 6,28 másodperc?

A: 320 B: 321 C: 322 D: 323

Péter 317 pontot kapott. Az alábbiak közül válassza ki Péter időeredményét!

A: 2 perc 7,00 mp B: 2 perc 7,60 mp C: 2 perc 7,80 mp D: 2 perc 8,00 mp

Az öttusa lovaglás számában egy akadálypályán tizenkét különböző akadályt kell a versenyzőnek átugratnia. Egy akadály a nehézsége alapján három csoportba sorolható: A, B vagy C típusú. Ádám a verseny előtti bemelegítéskor először az öt darab A, majd a négy darab B, végül a három darab C típusú akadályon ugrat át, mindegyiken pontosan egyszer. Bemelegítéskor az egyes akadálytípusokon belül a sorrend szabadon megválasztható.

d) Számítsa ki, hogy a bemelegítés során hányféle sorrendben ugrathatja át Ádám a tizenkét akadályt!

Megoldás

a) 278; b) 16; c) C, C; d) 17280